「挿絵画家になろう(その3)」です。
Blenderのアドオン、MB-Labの啓蒙です。
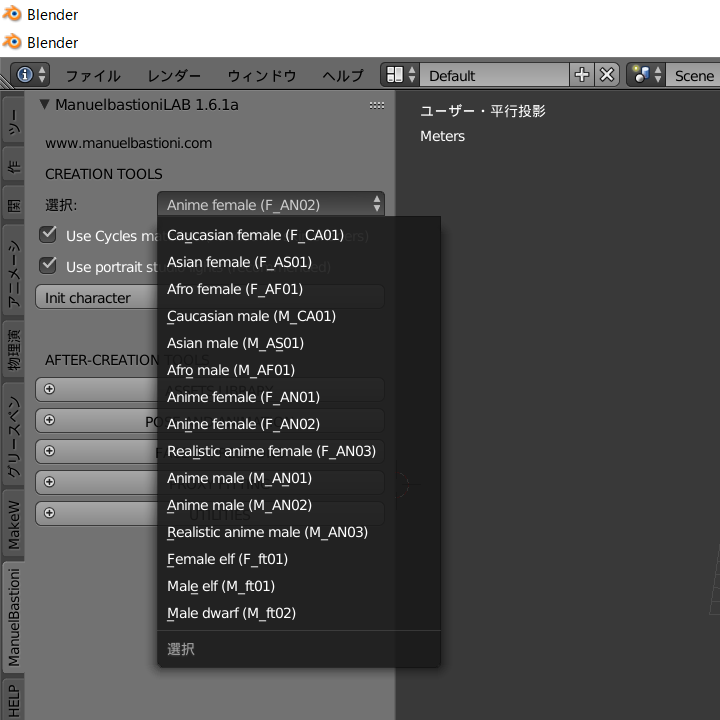
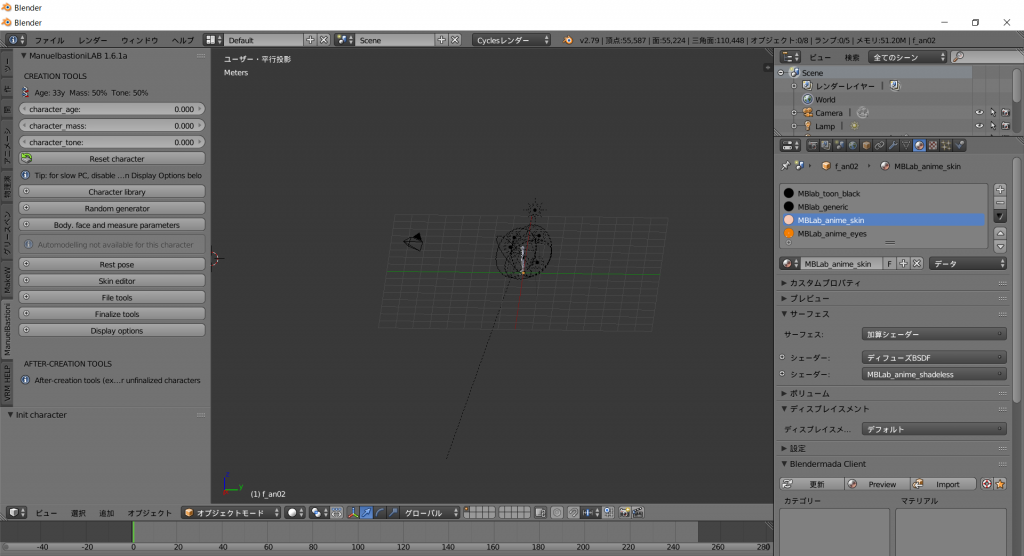
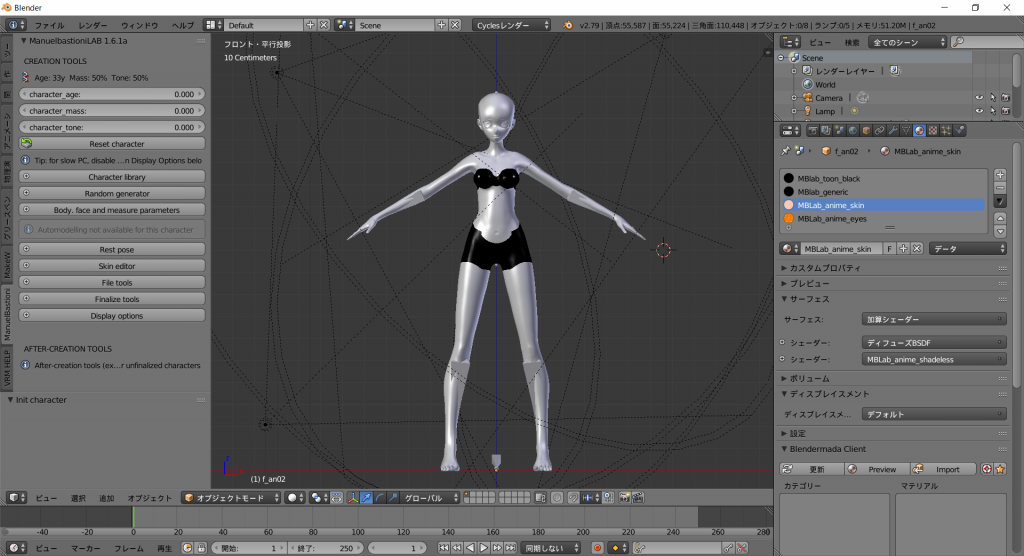
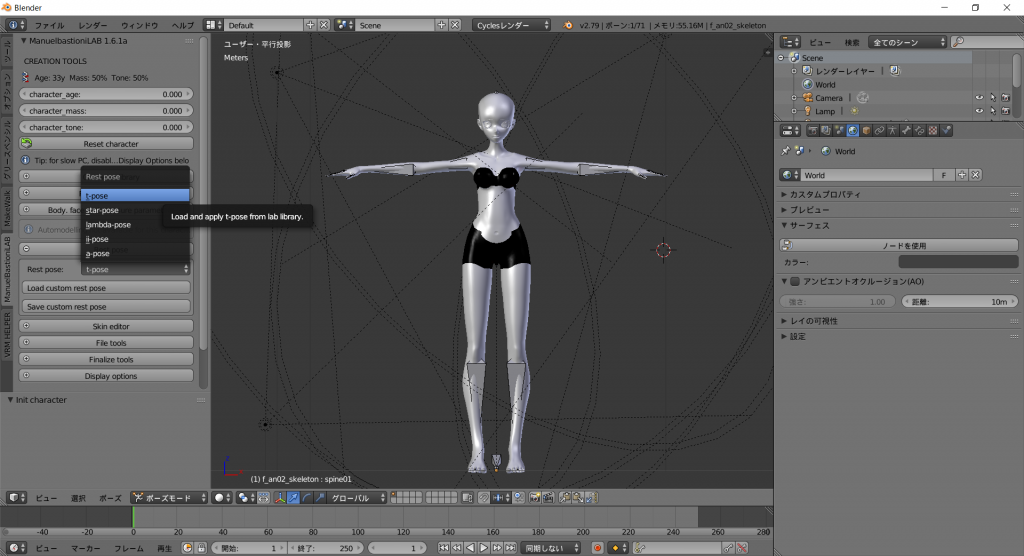
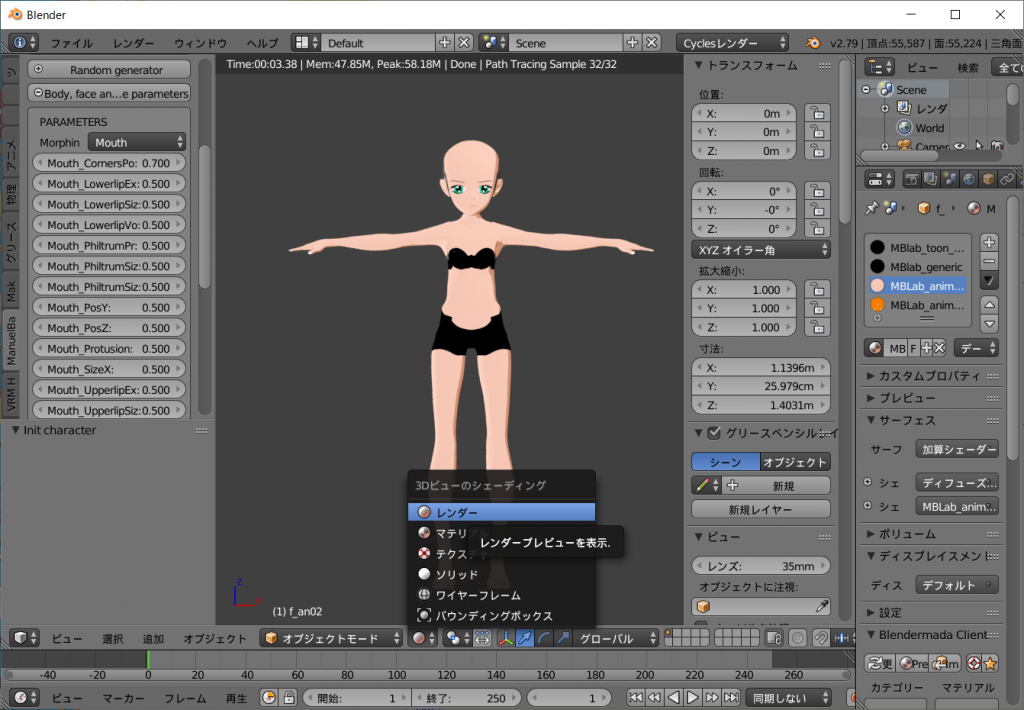
前回までで、MB-Labを使って少女キャラクターを生成し、簡素な服を着せ、あらかじめ用意されているポーズを切り替えるところまで実現しました。
今回は髪の毛です。
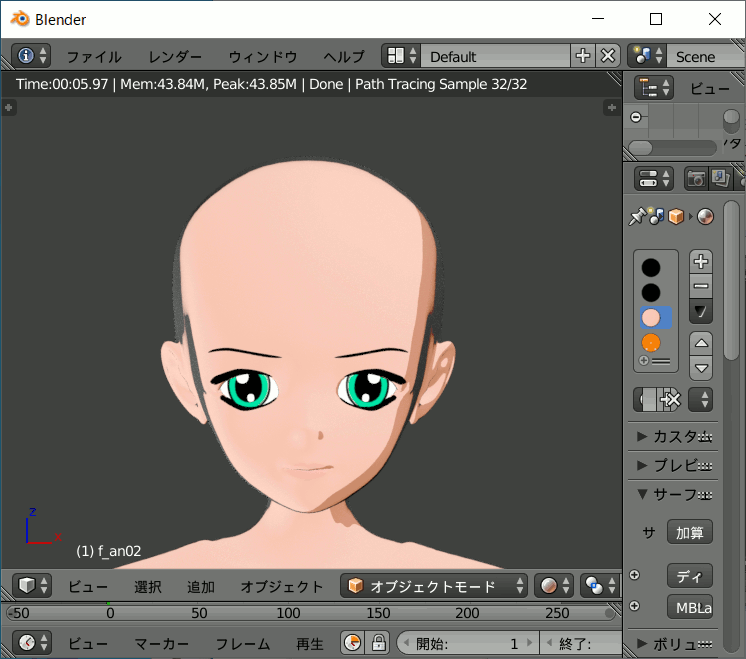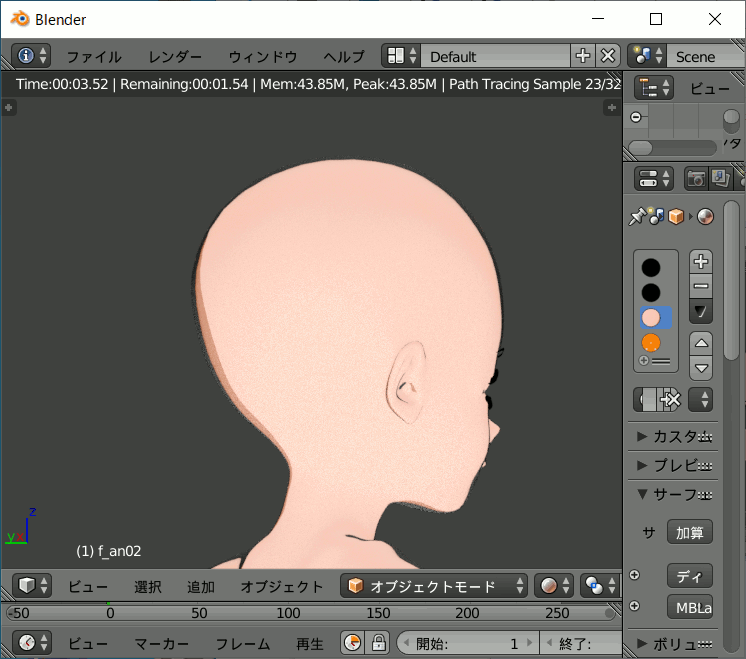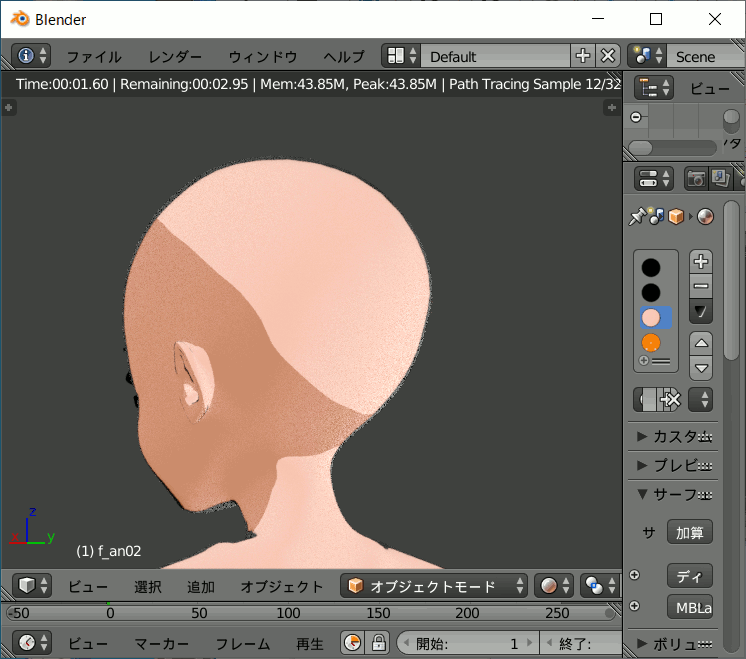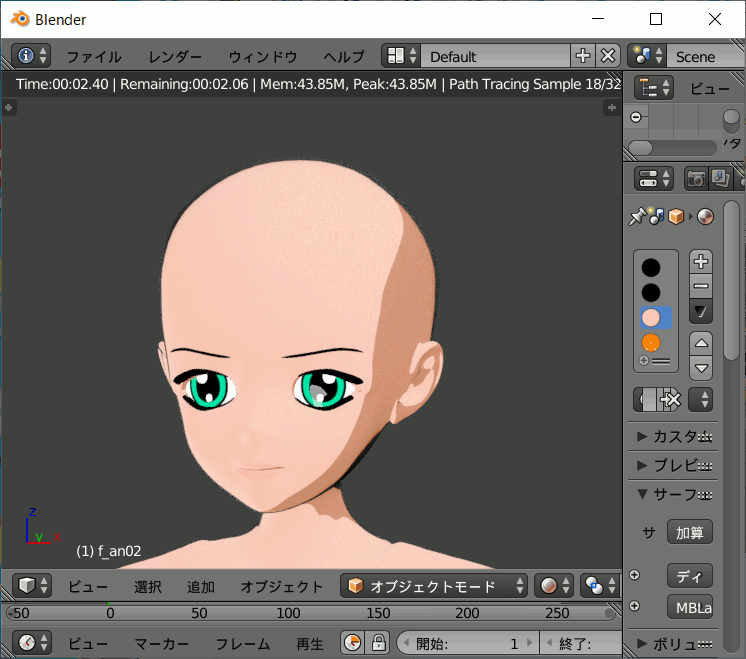
MB-Labにもアニメ調少年用、少女用の髪が一種類ずつ付属します。
それなりにクオリティが高いものですが、髪の毛はキャラクターの描き分けに必須です。
顔は同じで許すとして、髪の毛は異なるものを用意しないと人物の区別ができません。
私は髪の毛を用意するためにそれはそれはそれは色々な手法を試しました。
カーブという機能を使う方法、パーティクルを使う方法、UV球を変形させる方法、スカルプトでガチに造形する方法、その他色々……。
試しているうちに、Blenderの操作が少しずつ分かってきたのです。
費やした時間は膨大です。
その間、小説なんて全く執筆していません。
本末転倒なのです。
でもご安心ください。
この記事は『小説家になろう 』 としていて挿絵に困っている 同胞の諸兄姉に簡単に3Dキャラクターを使った挿絵を描く方法を展開することが目的です。
ソリューションがあるのです。
それは『VRoidStudio』という神アプリです。
Pixive 様に怒られそうですね。
VRoidStudioは髪型を作成するためのツールではありません。
Pixive様が開発・提供する3Dキャラクターモデル作成のための統合環境です。
寧ろMB-Labの競合ソフトです。
なにはともあれ、ゲットして試してみることをお勧めします。
本記事執筆時の最新版はVRoid Studio ベータ版 v0.7.3です。
起動するとキャラクターモデルの選択画面になります。
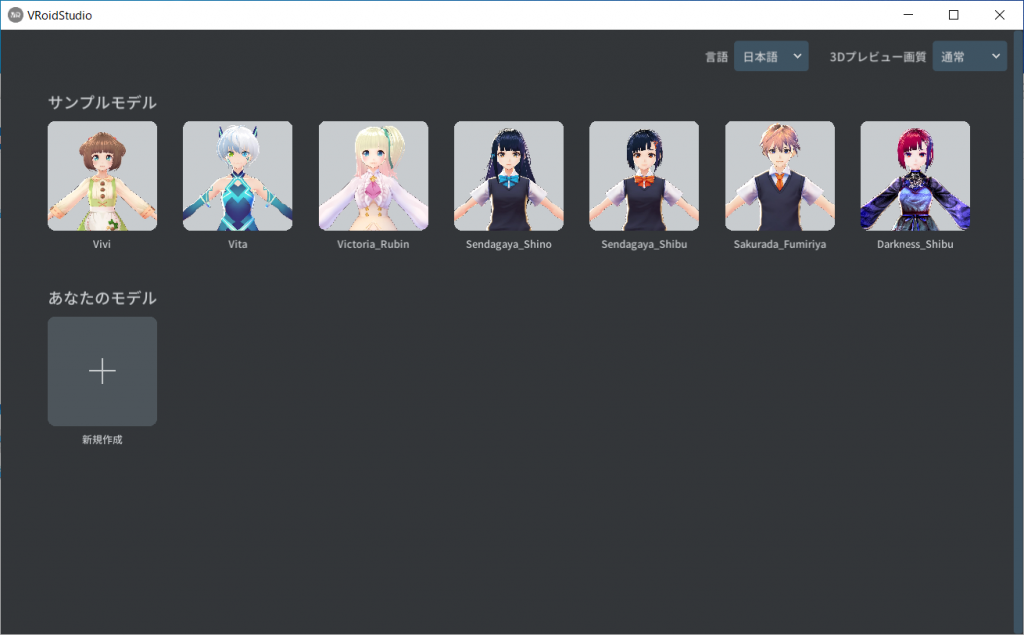
「あなたのモデル」として新規作成しても良いのですが、「サンプルモデル」として幾つかのサンプルモデルが選べるようになっています。
今回はSendagaya_Shinoを選びましょう。
これだけの操作で3Dキャラクター生成完了です。
質問:顔の編集できるのですか?
回答:はいできます。
質問:髪型の編集、できるのですか?
回答:はいできます。
質問:服の編集、できるのですか?
回答:いくつかの基本形があり、それぞれ変形させることができます。
テクスチャを差し替え、印象をがらりと変えることができます。
質問:ポーズの変更とかできるのですか?
回答:いくつかのプリセットから選べます。
VRM形式で描きだすことができるので、『3tene(ミテネ)』等の別ソフトにエキスポートすることもでき、それでポーズをつけることもできます。
質問:あれ? 挿絵のキャラクター作るのって、VroidStudioで良くね?
そのとおりです。
『VRoidStudio』はバーチャルユーチューバーなどにも使える優れたソフトです。
実際にVChatやバーチャルユーチューバーに使われていて、その実用性は折り紙付き。
ではなぜVRoidStudioを使わずにMB-Labを使うのか?
MB-Labの人体メッシュへの愛、所以です。
それにVRoidStudioがいかに良いソフトであるかなんて、今更私が力説してもね……。
細かくは、VRoidStudioは顔に関してそれほど多くのバリエーションを持ちません。
メッシュが破綻するようなダイナミックな調整はできないのです。
恐らくはVRoidStudioの範囲内で留まる限り、defaultの表情からそれほど離れることはできないでしょう。
カスタムキャスト で作ったモデルが、カスタムキャストで作ったと判るように、VRoidStudioで作ったモデルも同様のことが言えそうです。
とはいえ、BlenderもVRM形式のデータを読み込む方法が無いわけではなく、一旦読み込んでしまえばあとはどうとでも編集できてしまいます。
ただBlenderとの親和性とメッシュの弄りやすさには差がでるかと……。
もう一つ、服に画像テクスチャを張り付ける仕様です。
服の造形にはそれほど自由度がありません。
VRoidStudioのコミニュティでは服用のテクスチャの開発が盛んですが、テクスチャ作成は職人芸の世界だったりします。
3Dメッシュを弄るのとどちらがより楽かという天秤になります。
私はそれっぽい2Dテクスチャを作るスキルを今に至って培うことができていません。
正直この辺は得手不得手なのでしょうね。
とりあえず髪の話に戻します。
VRoidStudioでは髪を比較的簡単に編集できます。
なおかつ髪をOBJ形式でエクスポートすることができます。
Sendagaya_Shino のdefaultの髪の毛をOBJ形式でエクスポートしてみましょう。
上段二行目のタブから『撮影・エクスポート』を選択し、左側メニューの『エクスポート』を選択します。
すると右側に『髪をOBJ形式でエクスポート(四角形メッシュ)』が選択できるようになります。
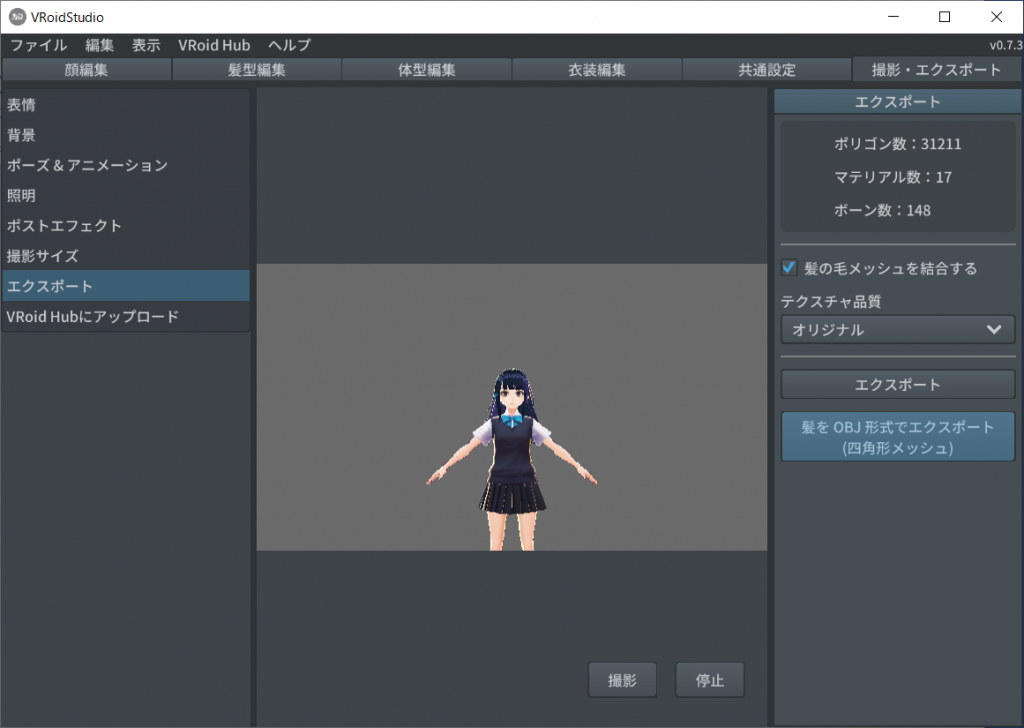
「Sendagaya_Shino_Hair.obj」というファイル名で保存してください。
次に前回MB-Labで作成したBlenderのプロジェクトにインポートします。
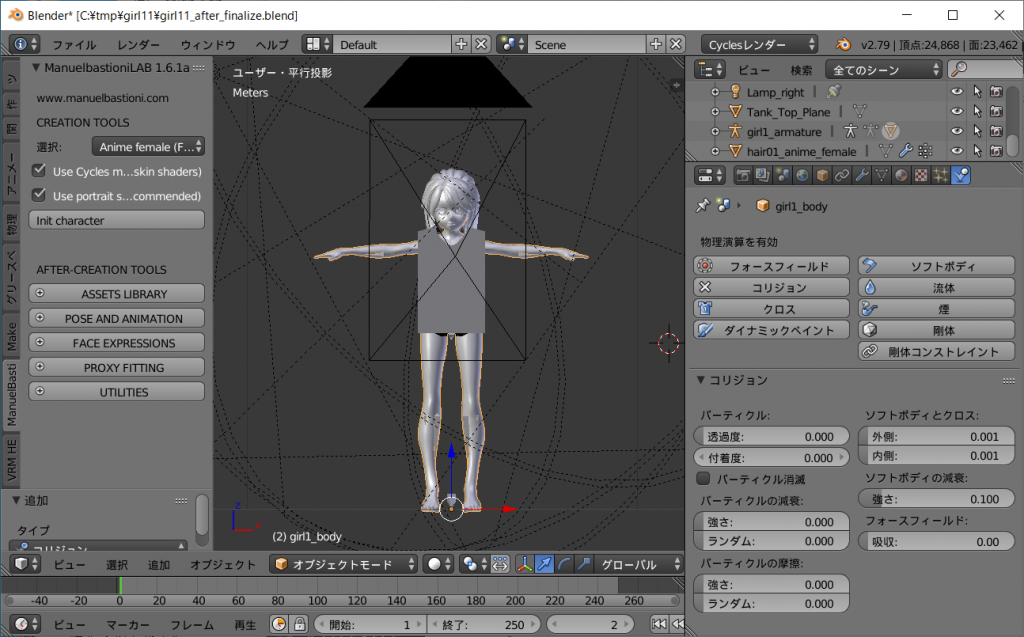
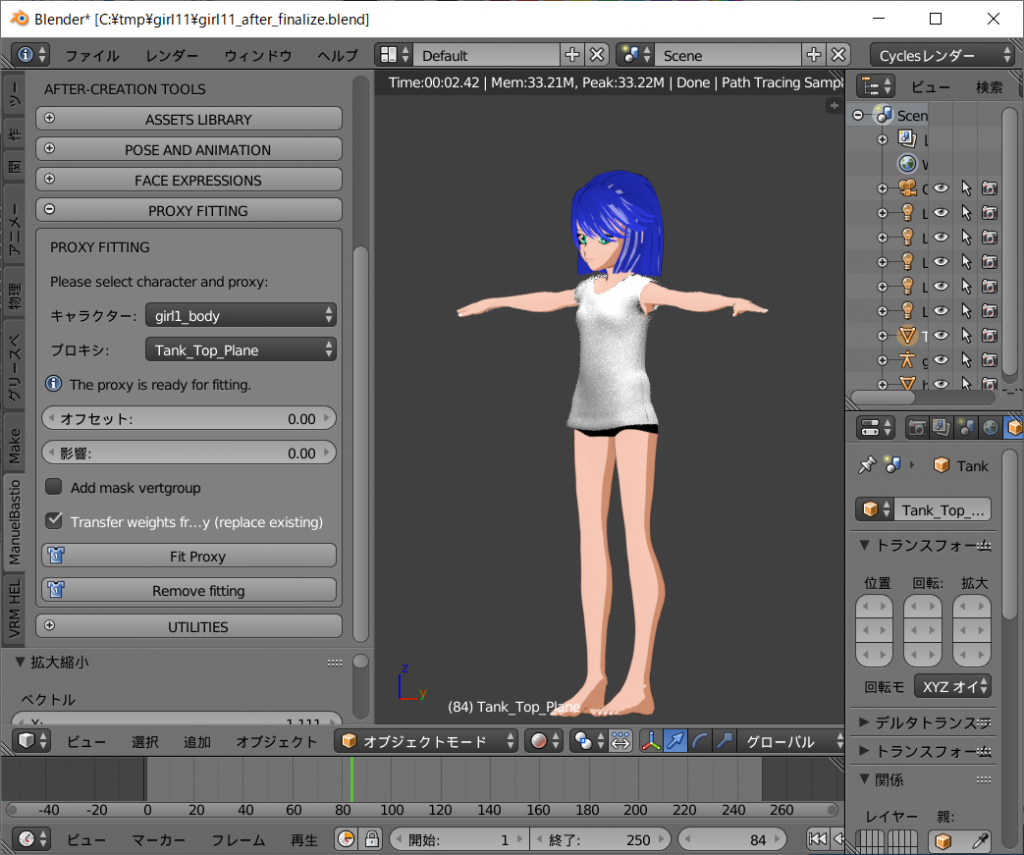
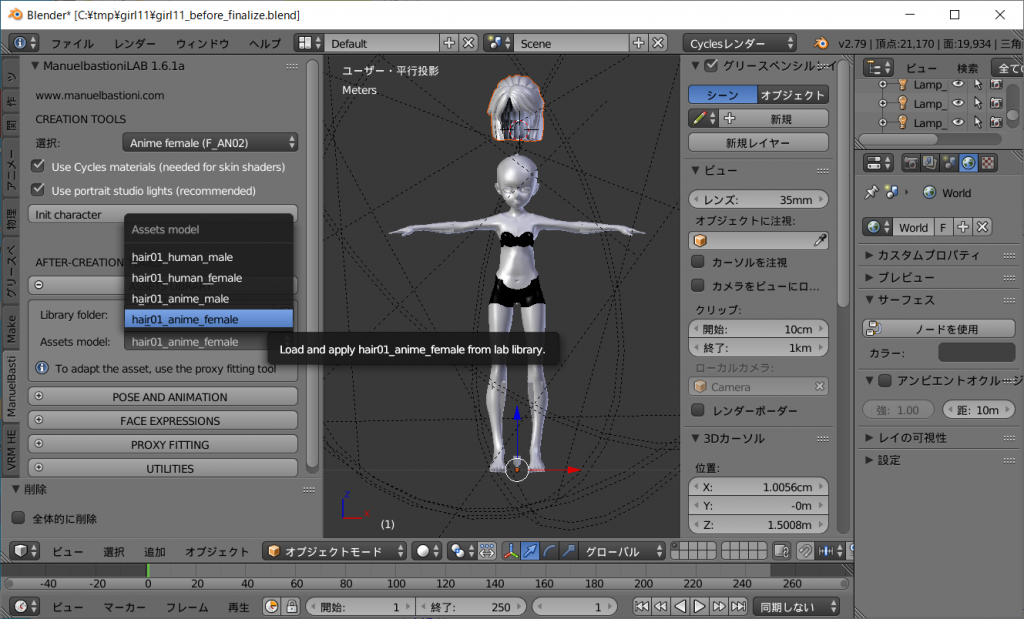
先ずはdefaultの髪を外します。
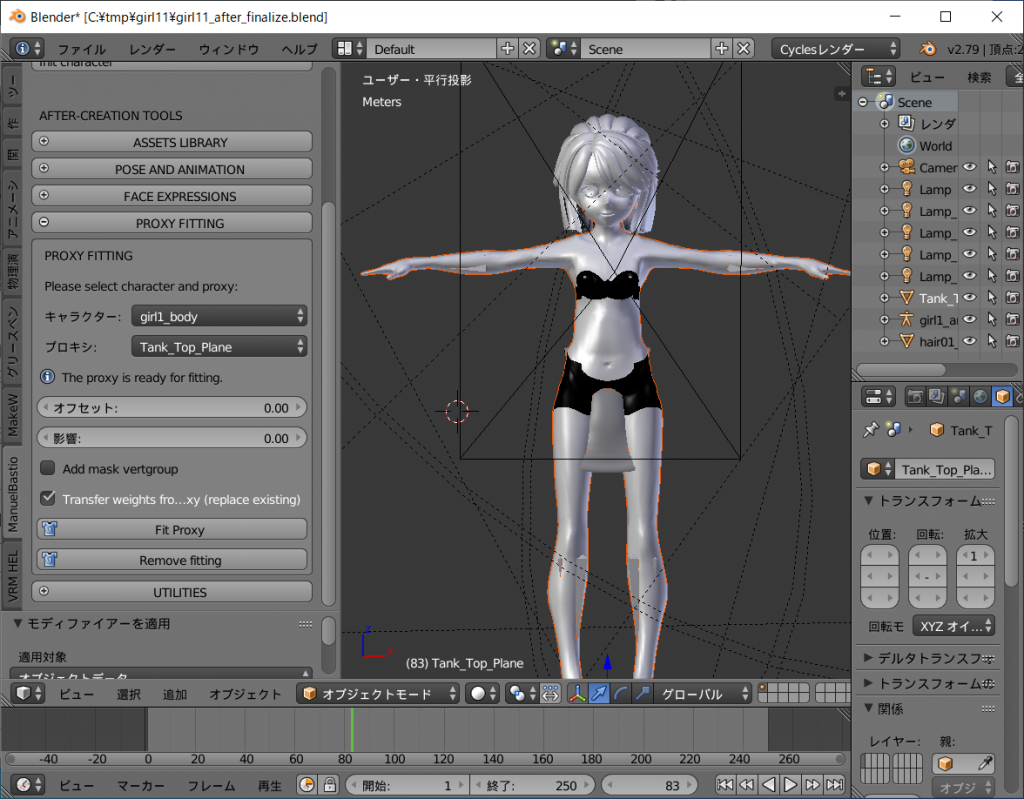
キャラクターの両足の間ににある横倒しになった四角錐を右クリックします。
そしてオブジェクトモードに切り替えます。
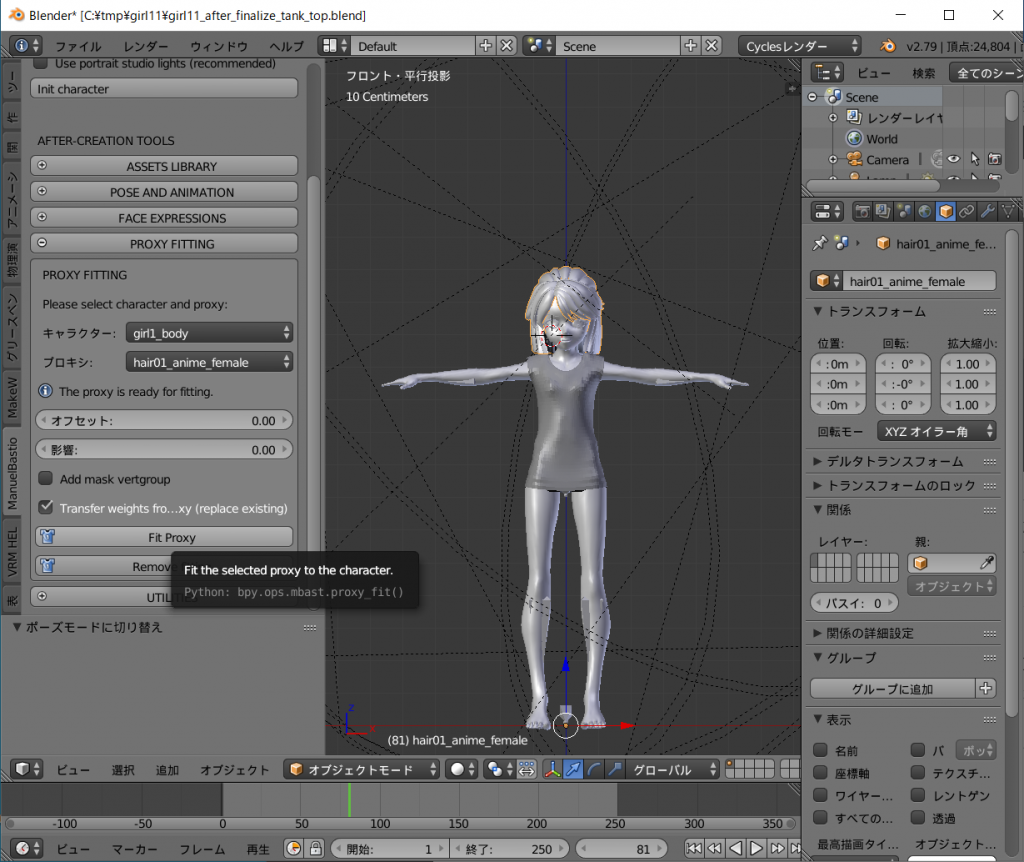
ツールシェルフの[ManuelBastioneLab]タグ、[PROXY FITTING]から[キャラクター:]をgirl1_bodyに、[プロキシ:]をhair01_anime_femaleを選択し、[Remove fitting]ボタンを左クリックします。
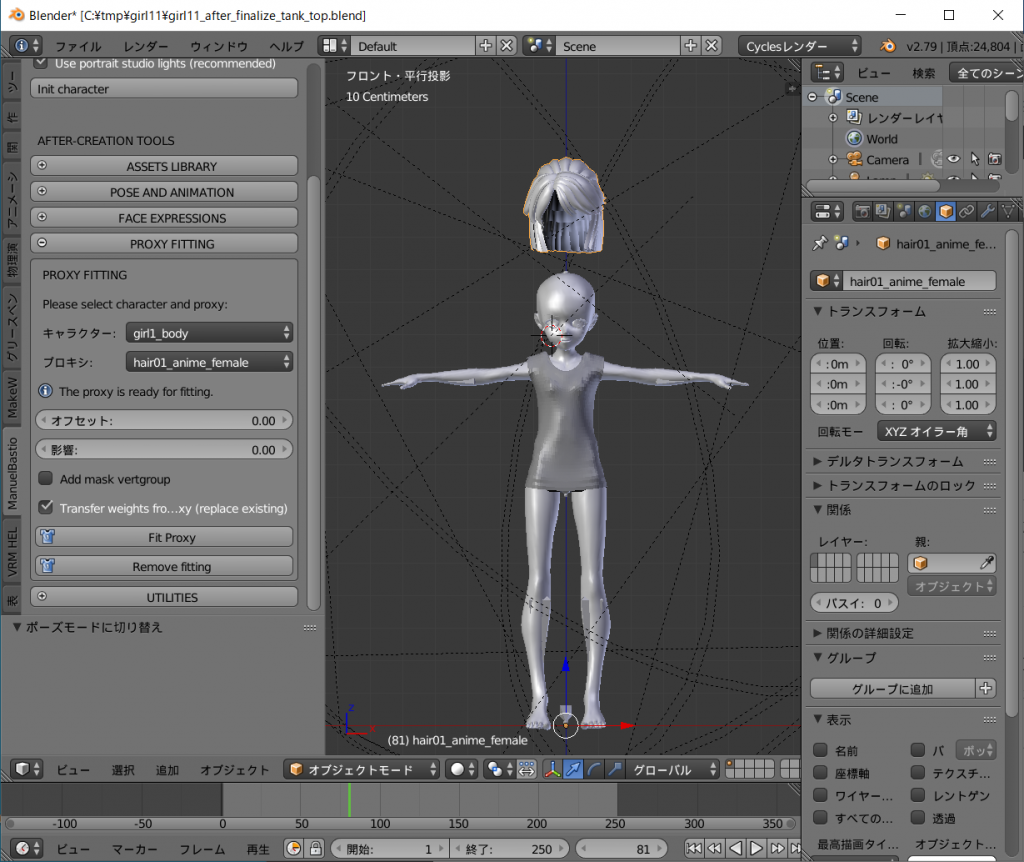
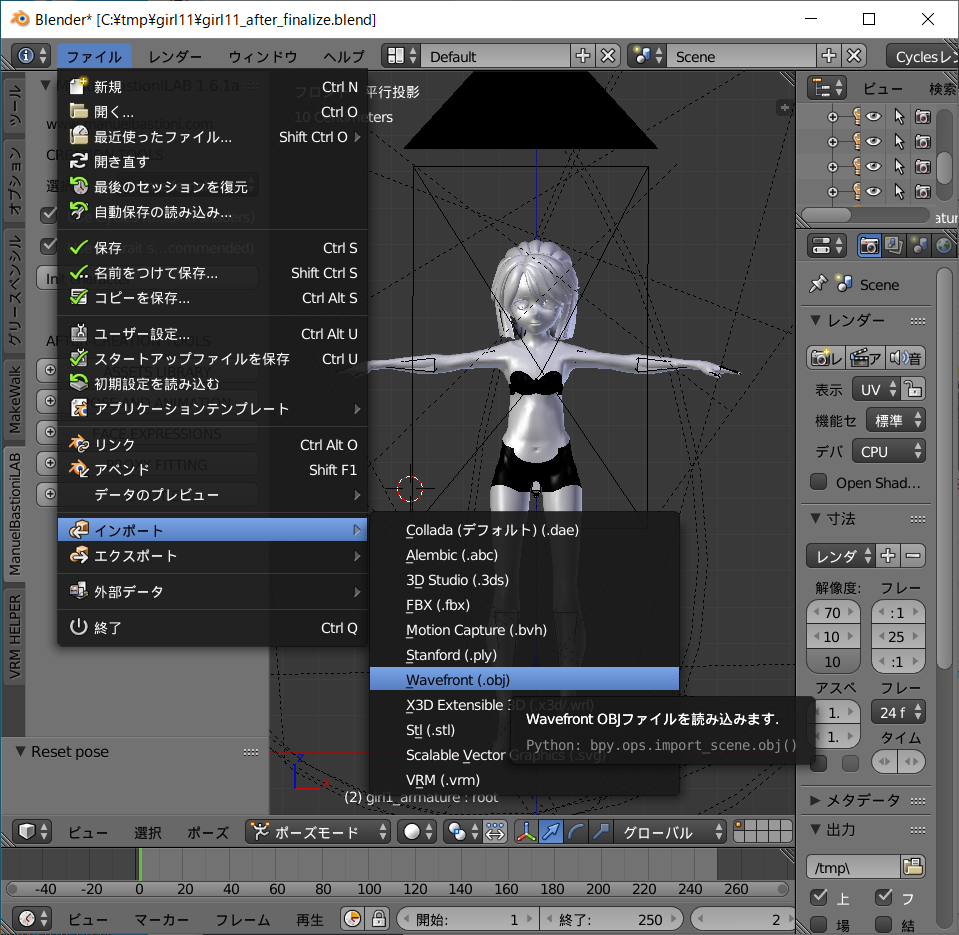
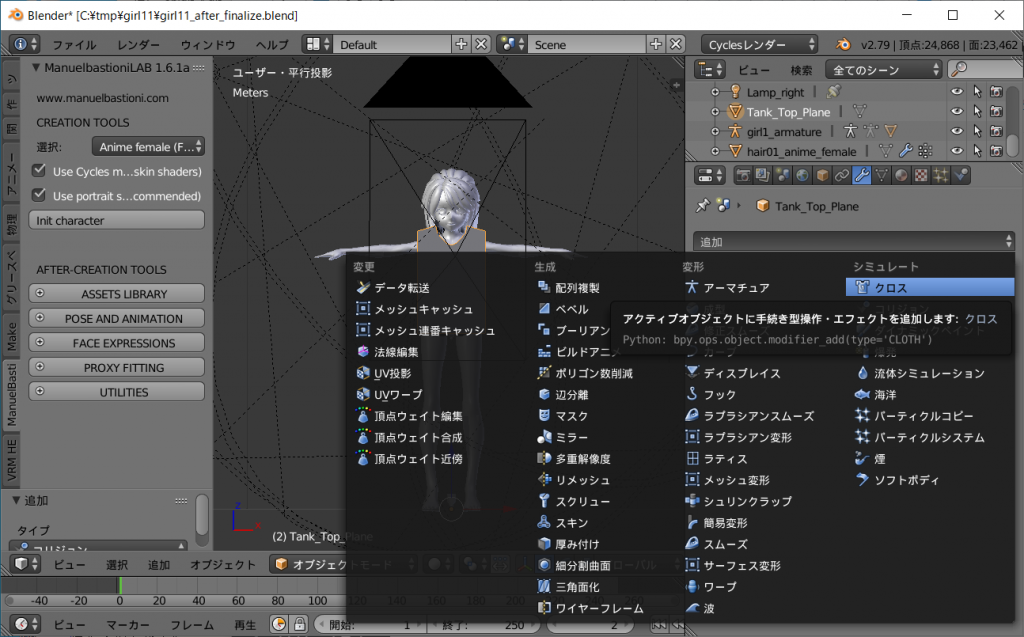
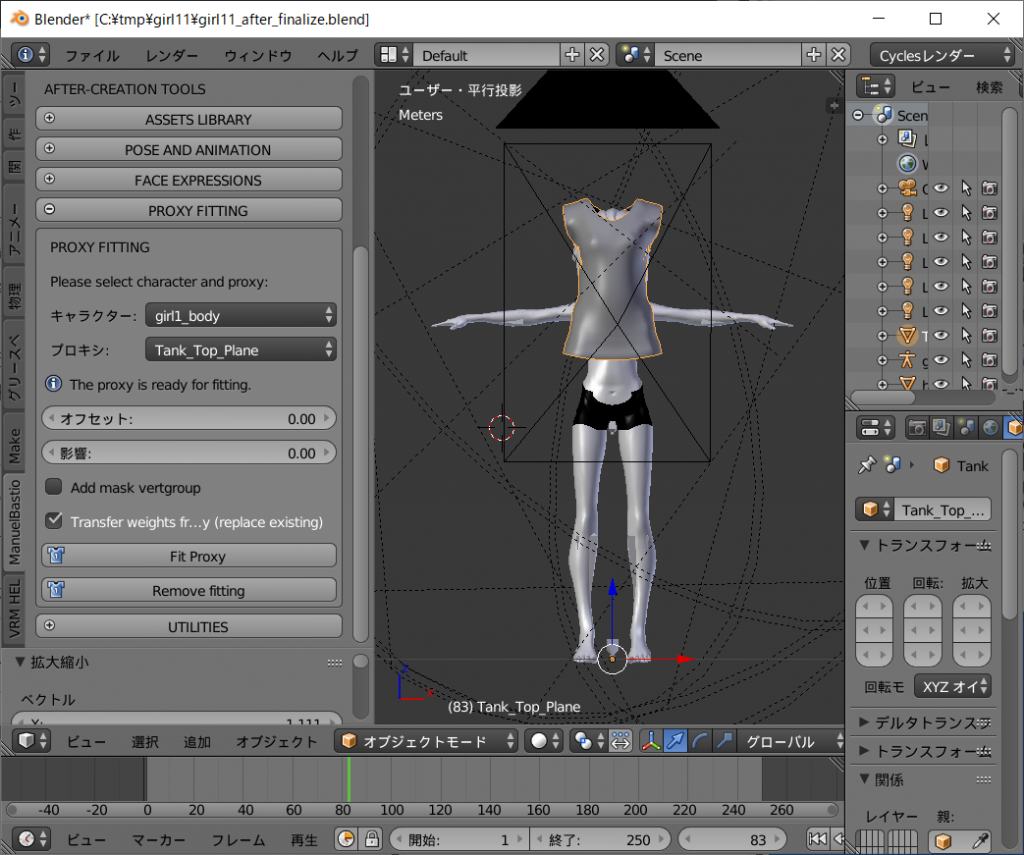
次に Sendagaya_Shino_Hair.obj をインポートします。
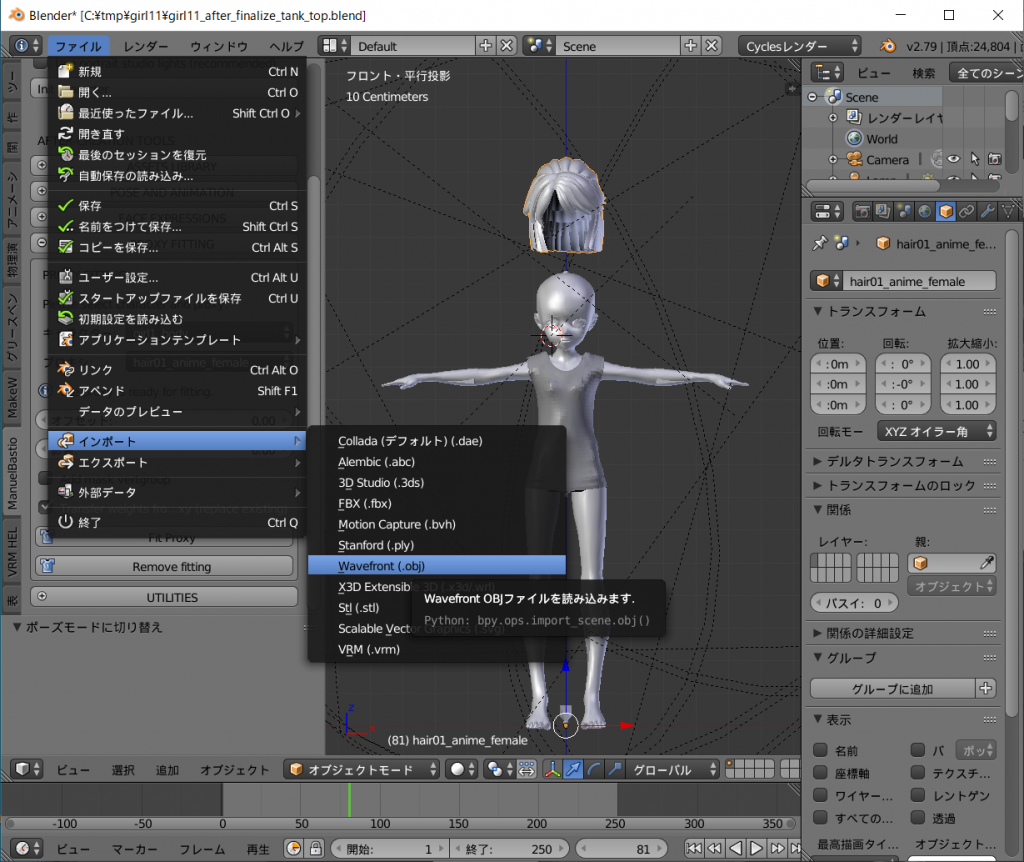
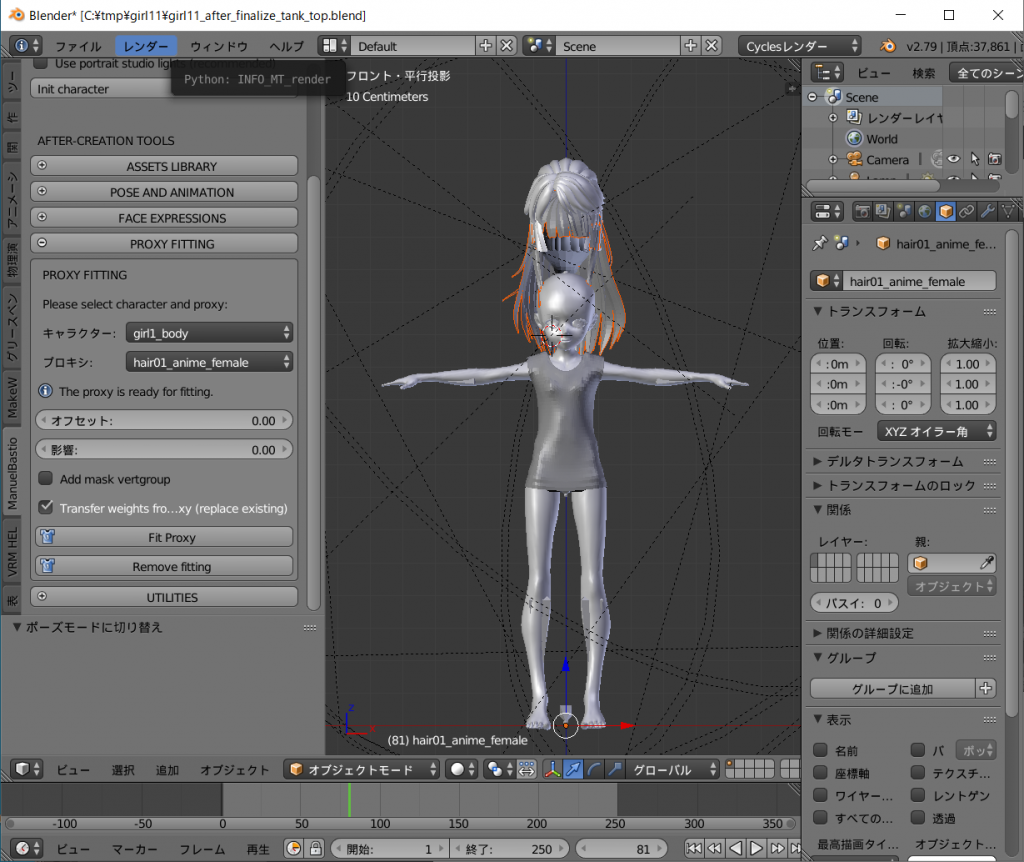
Sendagaya_Shino_Hairがdefaultの髪と重なって出現します。
オレンジ色に縁どりされ、選択された状態になっていると思いますが、選択されていなければ右クリックで選択してください。
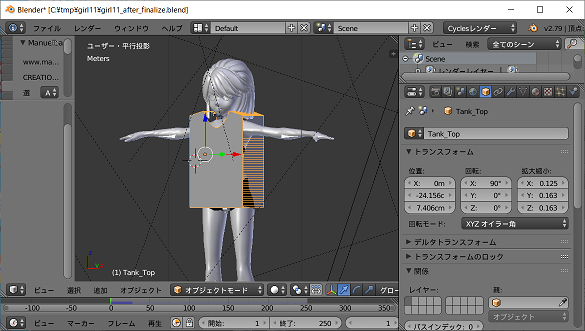
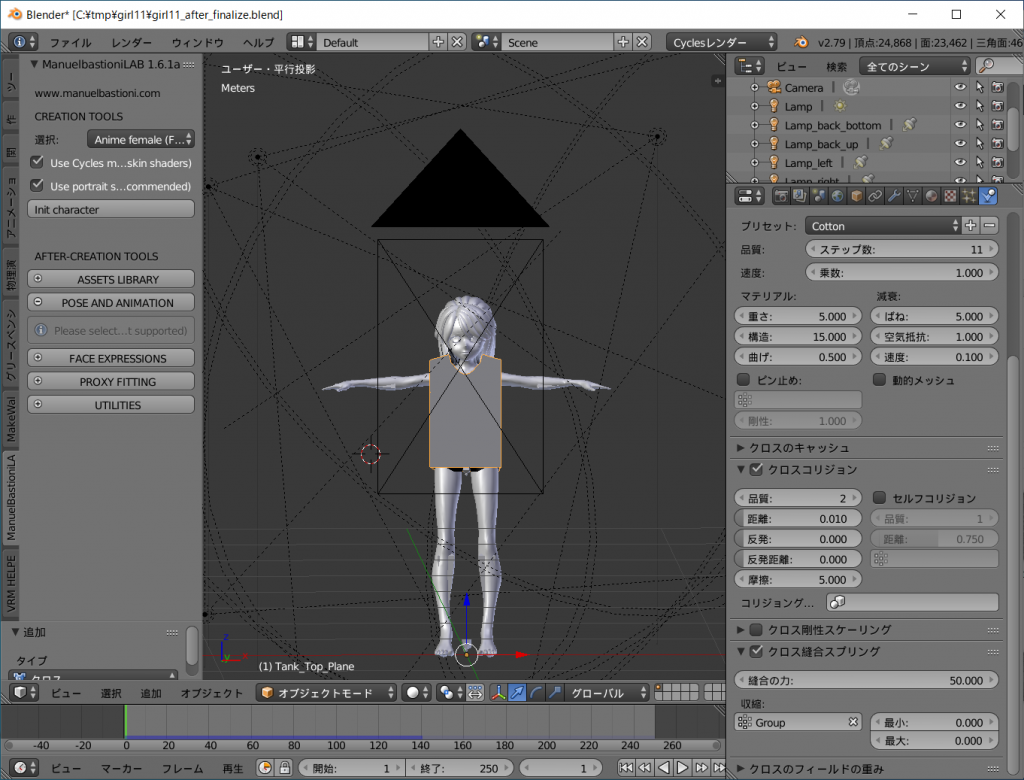
Sendagaya_Shino_Hair の位置合わせを行います。
defaultの髪とほぼ同じ位置に重なるようにすればOKです。
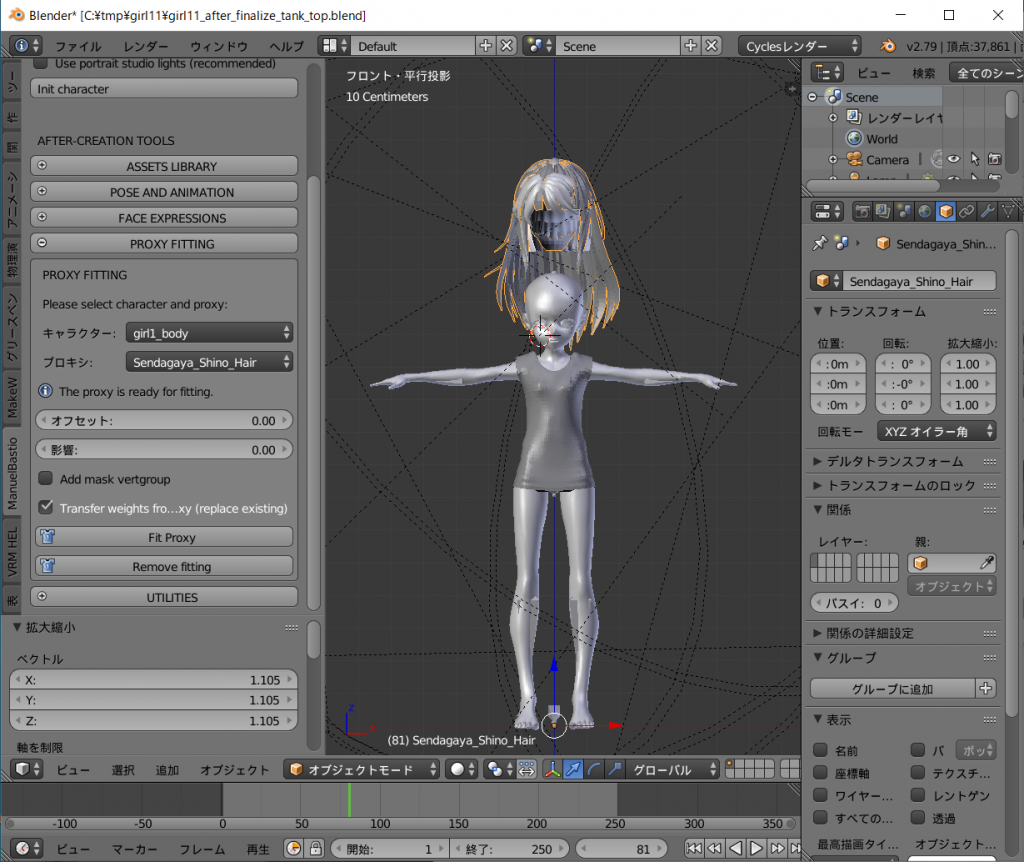
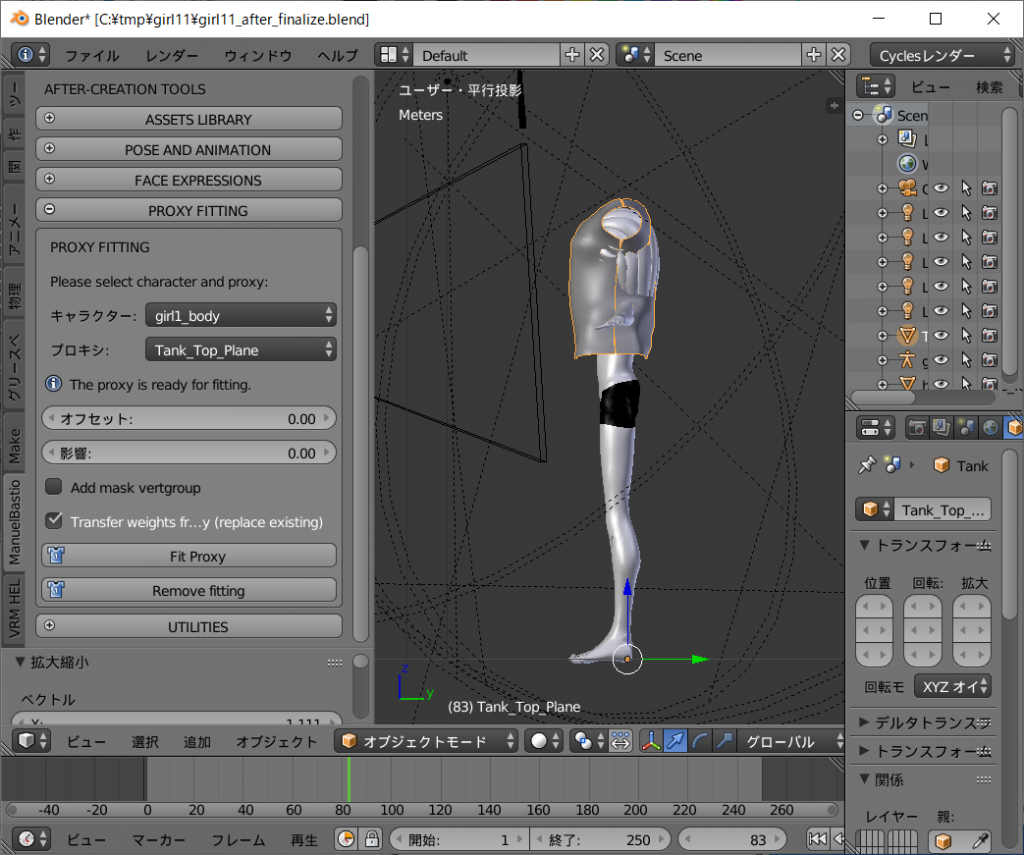
Sendagaya_Shino_Hair を上への拡大([s]キーに続き[z]キー、後は[↑]キーで調整し[enter]キーで確定)、左右への拡大 ([s]キーに続き[x]キー、後は[←]キーで調整し[enter]キーで確定)、前後への移動 (テンキーの[3]キーを押して横にして、[g]キーに続き[y]キー、後は[←]キーで調整し[enter]キーで確定)等で調整します。
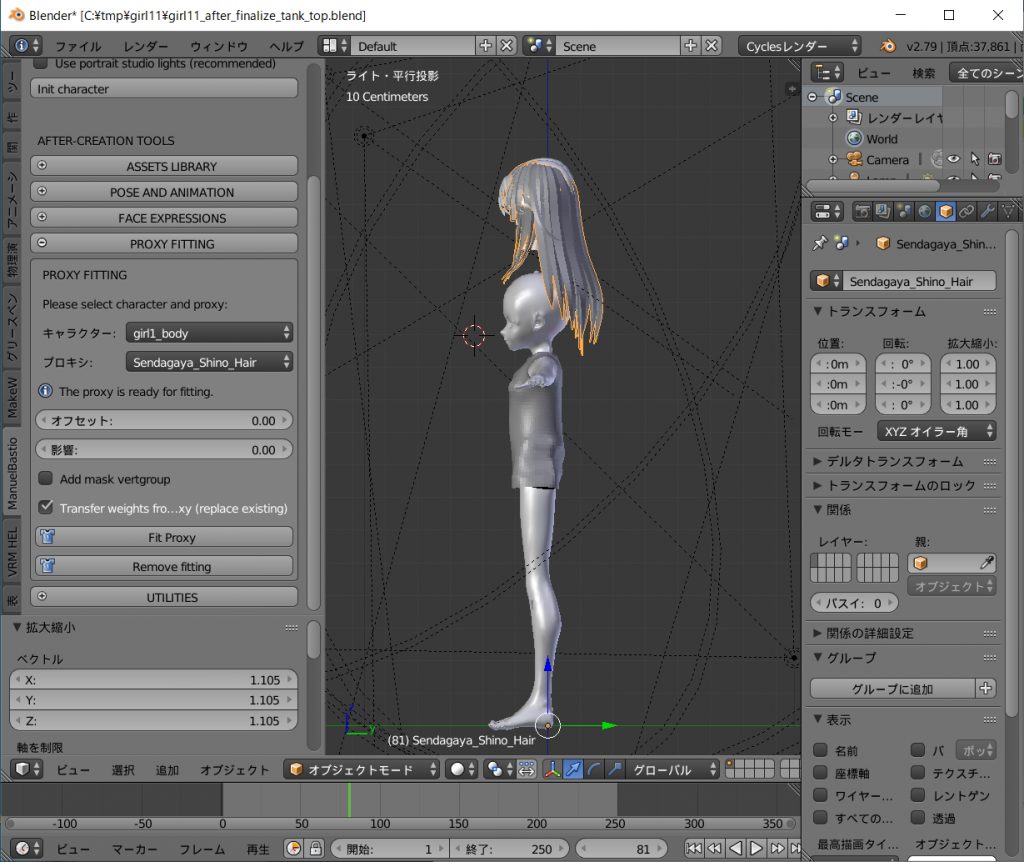
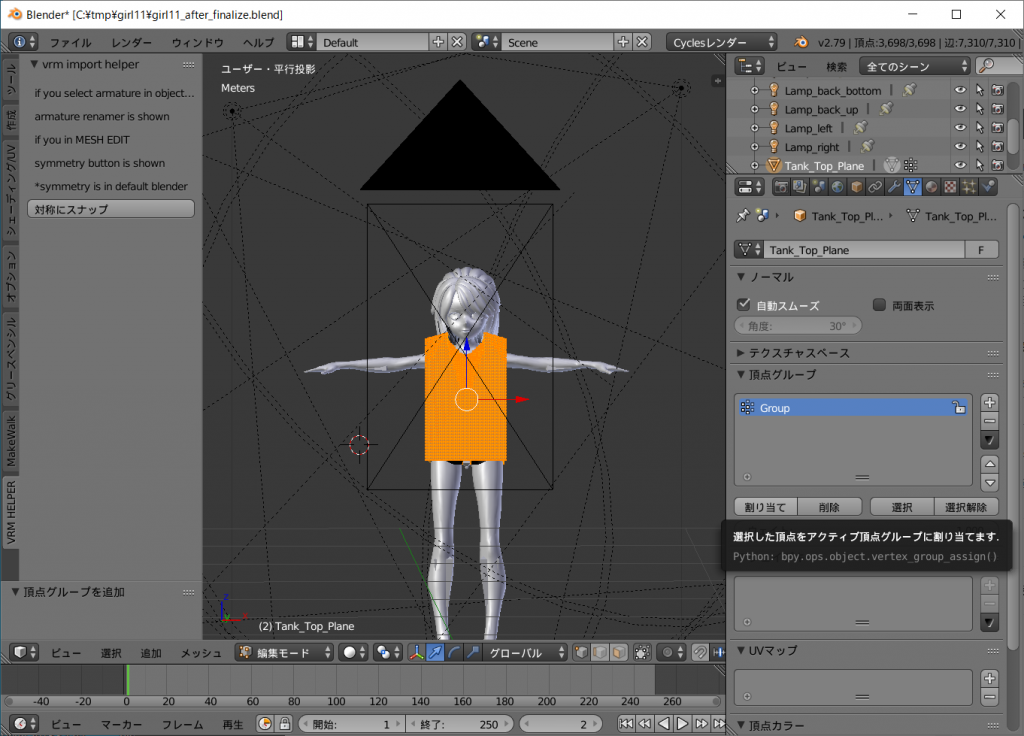
できましたらテンキーの[1]キーを押して正面を向かせ、PROXYシステムで装着します。
ツールシェルフの[ManuelBastioneLab]タグ、[PROXY FITTING]から[キャラクター:]をgirl1_bodyに、[プロキシ:]をSendagaya_Shino_Hairを選択し、[Fit Proxy]ボタンを左クリックします。
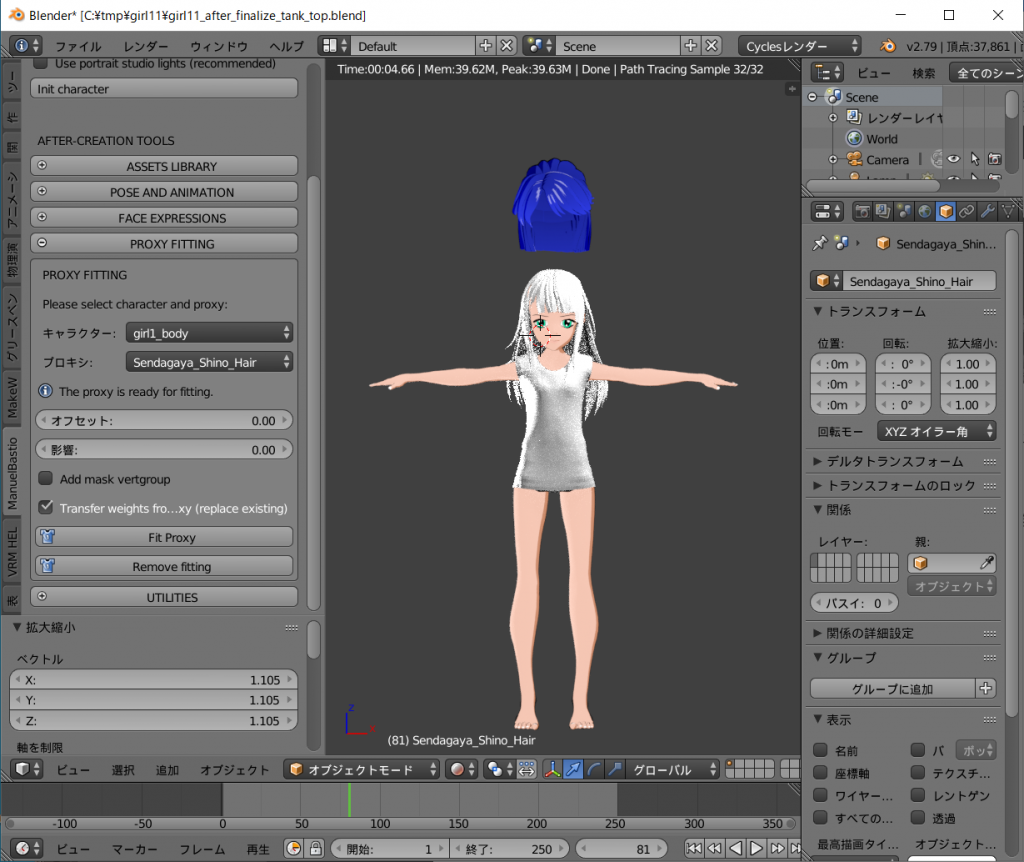
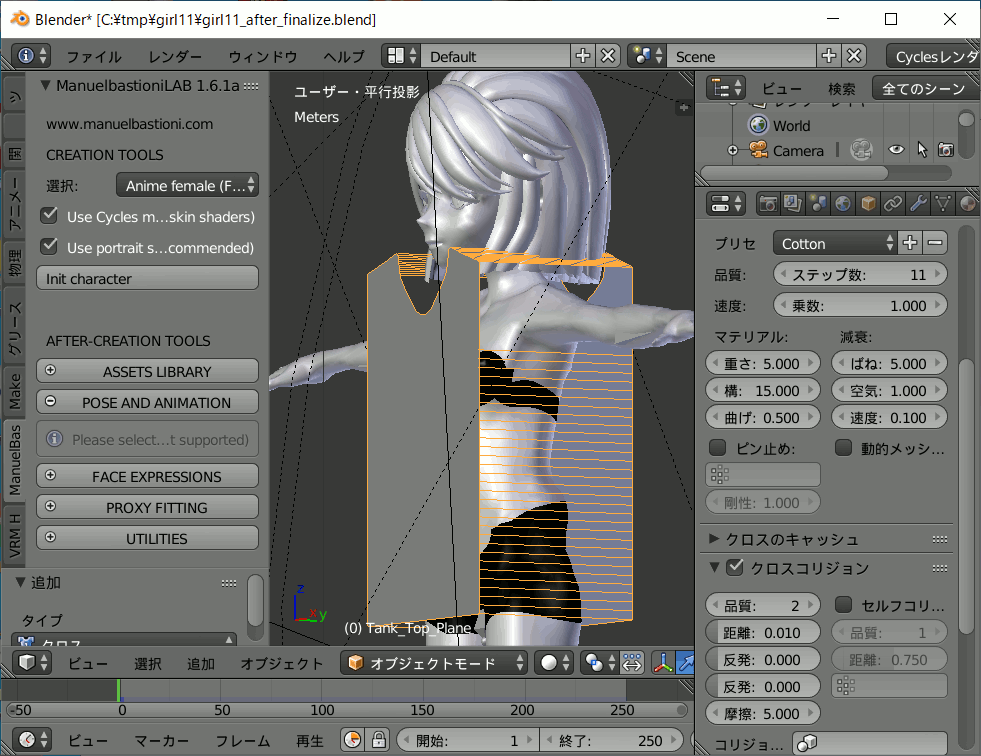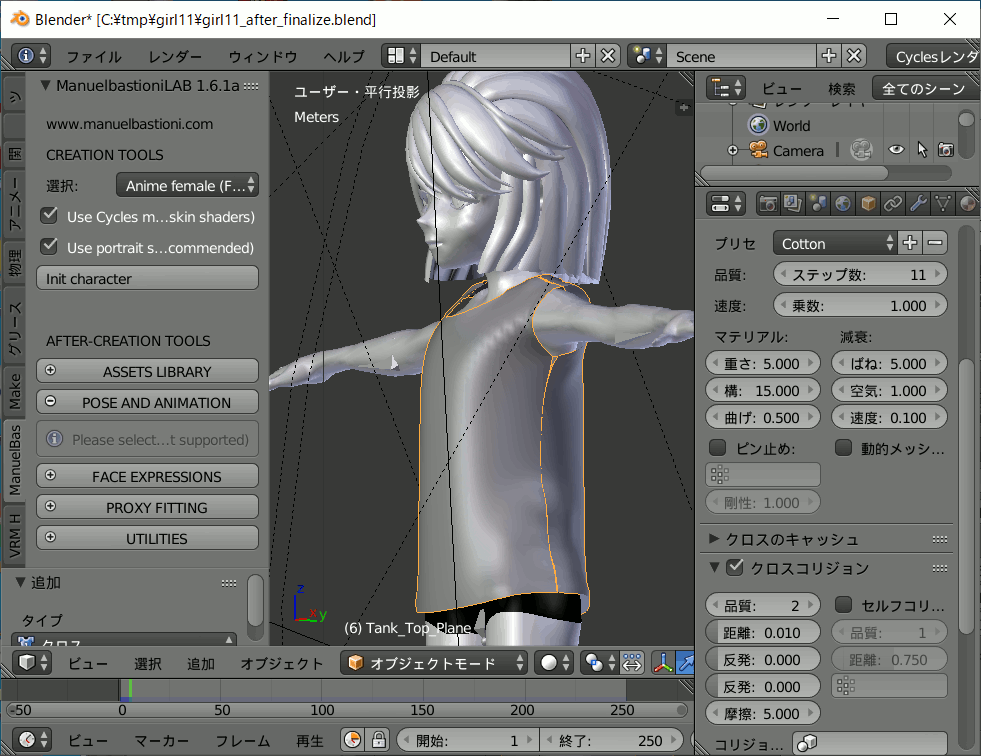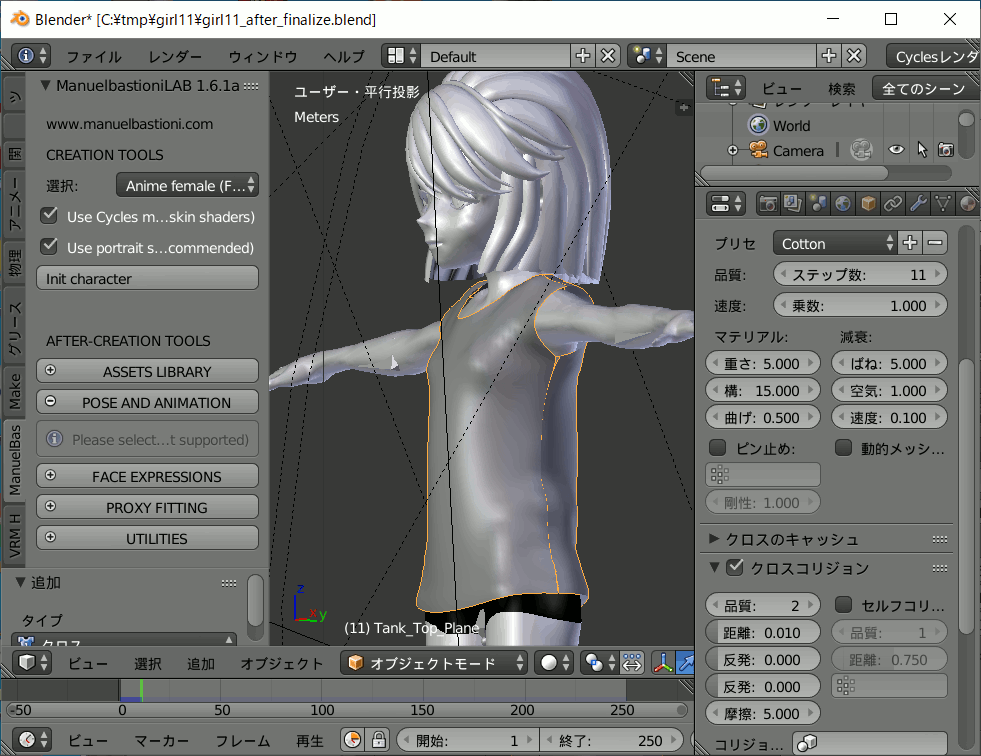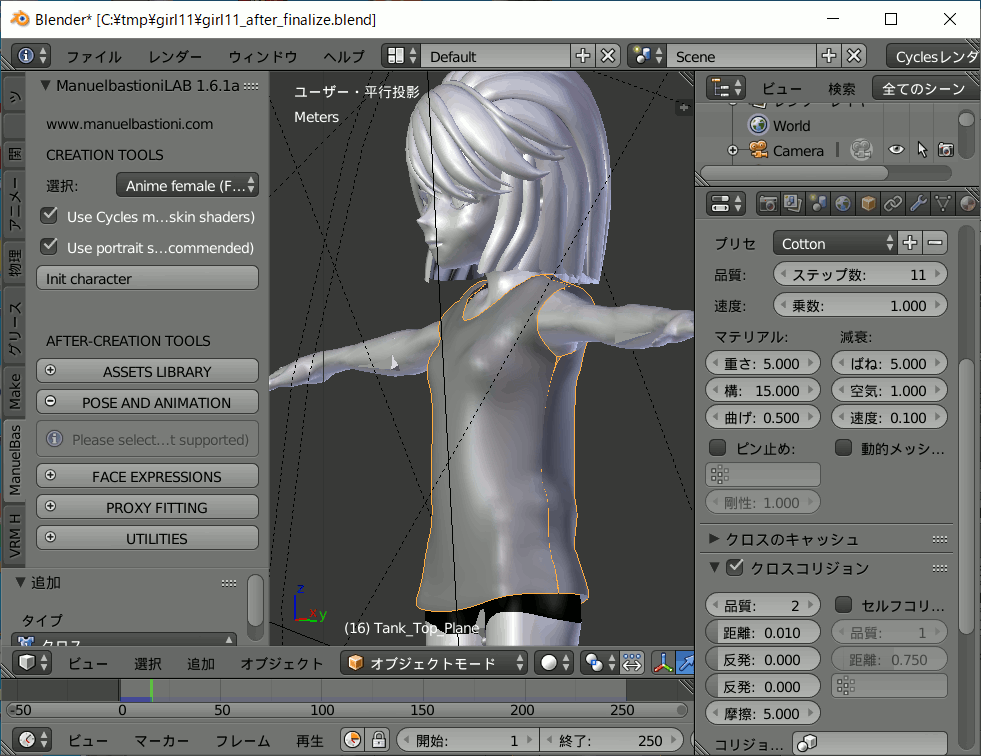
おお! 髪よ! フィットしました。
しかも輝くばかりの銀髪。
VRoidStudioとMB-Labとのキャラクター造形の違いにより前髪が眉上になってしまっていますが、これはこれでいいではないでしょうか?
気になる方は、髪を上下に拡大してから位置合わせをすると好みに合わせることができます。
髪の毛が銀色なのは袖なしTシャツ同様、マテリアルを設定していないからです。
Sendagaya_Shino_Hairオブジェクトにdefaultの髪のマテリアルを設定してみましょう。
オブジェクトモードになっていることを確認してから、Sendagaya_Shino_Hairを右クリックして選択します。
プロパティウインドウのマテリアル(赤と白の十字の円のマーク)を選択します
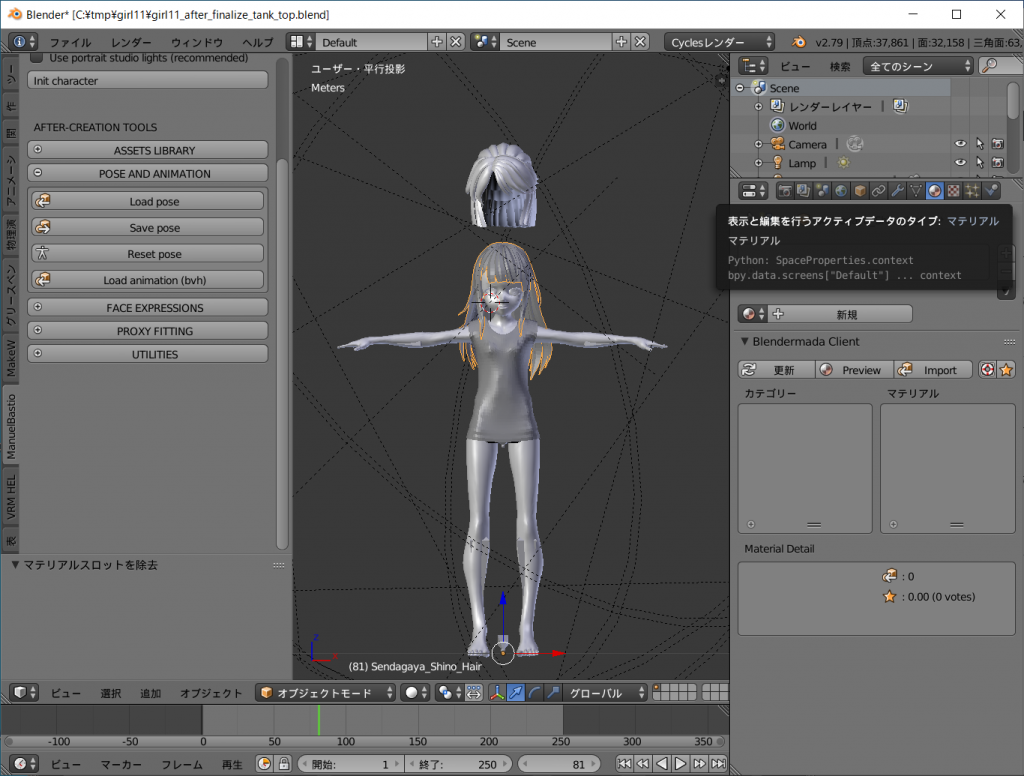
Sendagaya_Shino_Hairの項目の下、空の長方形の右の[+]ボタンを押して新しいマテリアルスロットを追加します。
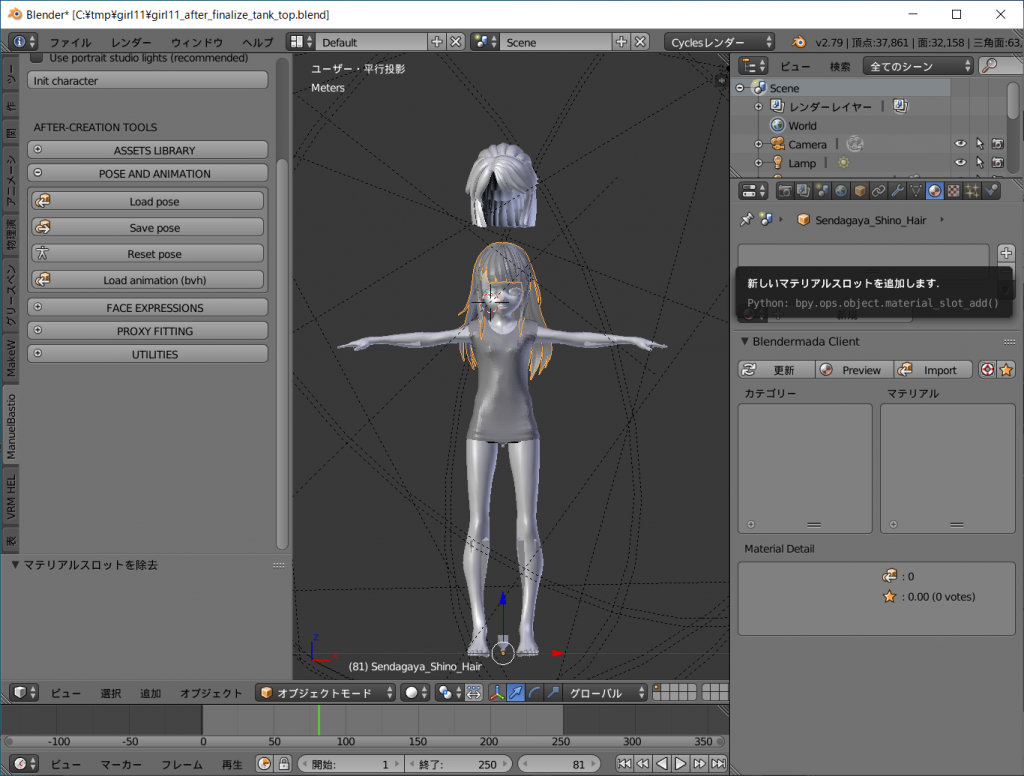
新しいマテリアルスロットが現れるので[新規]となっているマテリアルのセレクターボタン([△]ボタンもしくは[▽]ボタン)を押して既存のマテリアルリストを表示させます。
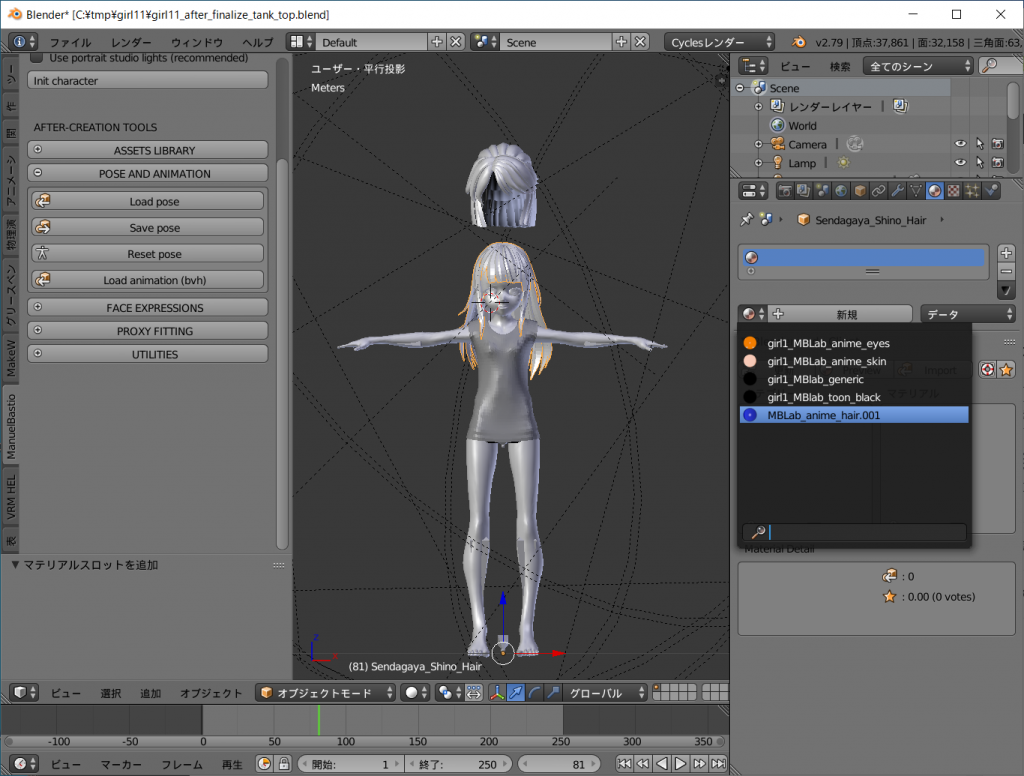
MBLab_anime_hair_001を選択してください。
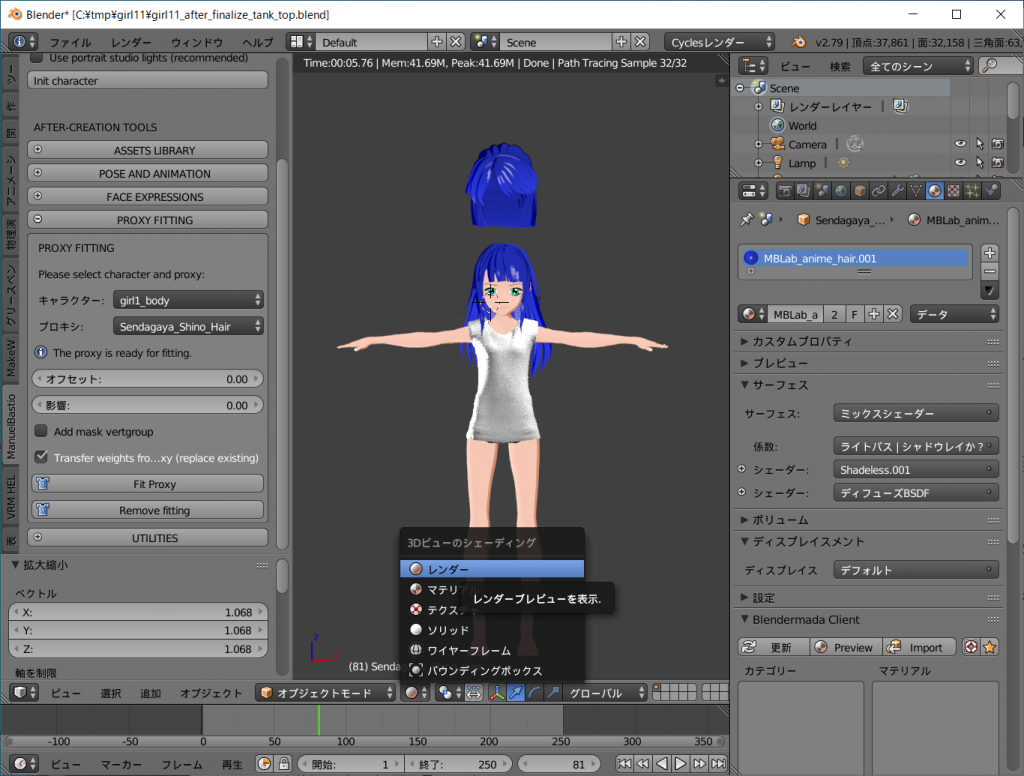
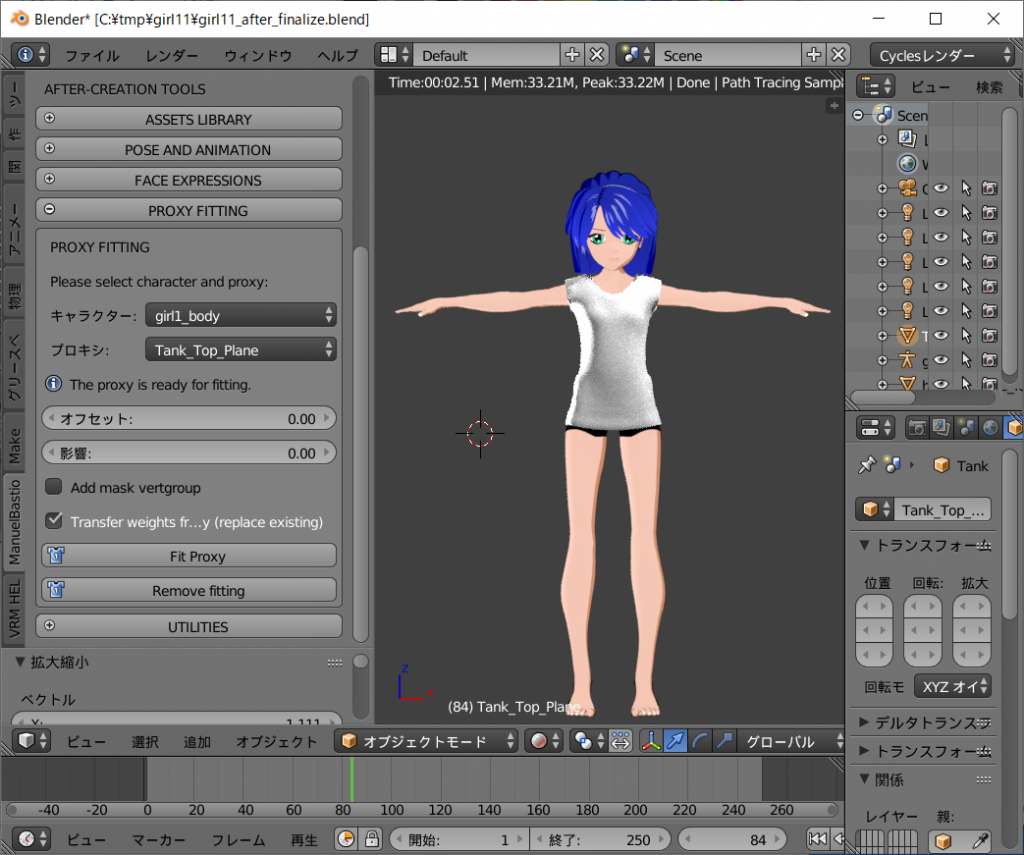
艶のある青髪になりました。
defaultの髪は不要になりますので削除します。
オブジェクトモードになっていることを確かめて、hair01_anime_femaleオブジェクトを右クリックして選択し、[delete]キーを押下します。
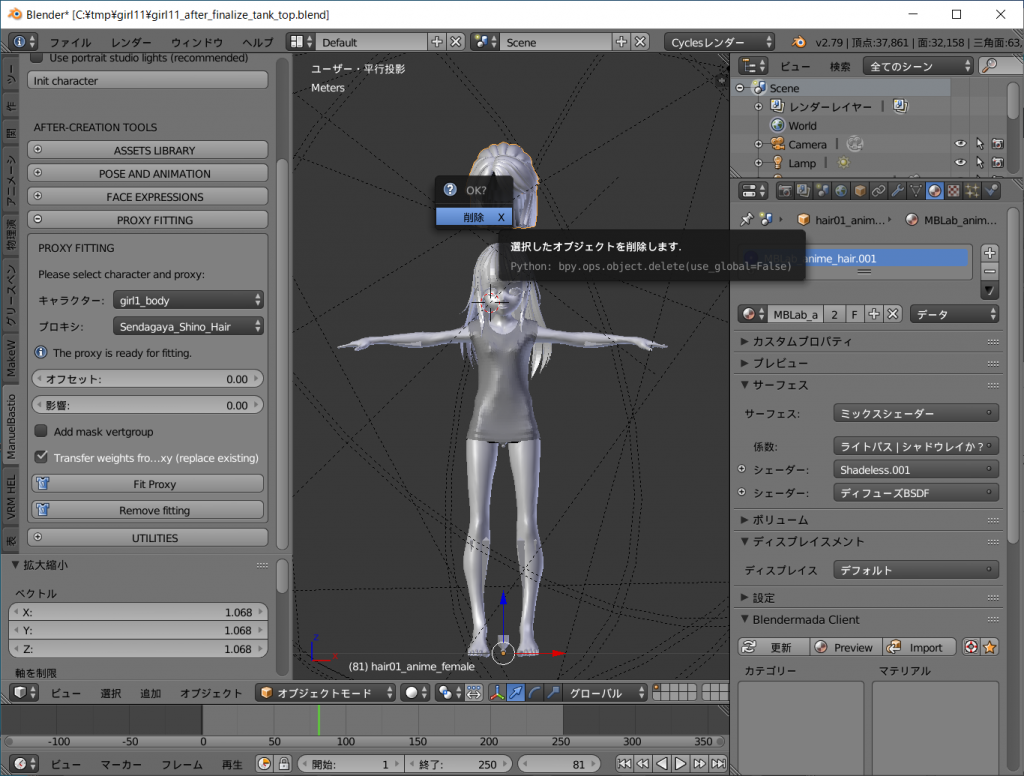
OK? と聞いてくるので[削除 X]ボタンを左クリックすると削除できます。
ついでに袖なしTシャツのマテリアルを設定します。
オブジェクトモードになっていることを確認し、上にあるViewのセレクタ([Default]となっている横の[△]ボタンか[▽]ボタン)を右クリックして現れる選択肢から[Composing]を選択します。
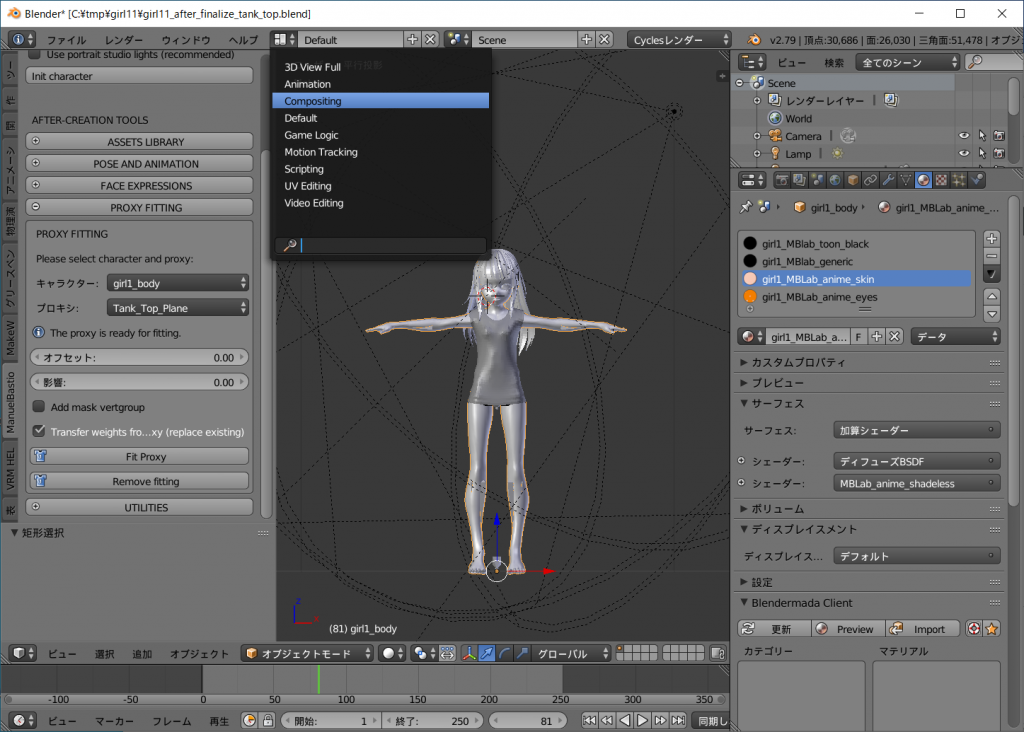
下にある3Dビューエディッタウインドウでgirl1_bodyオブジェクト(キャラクターの手とか足)を右クリックして選択します。
その後上にあるノードエディッタウインドウの下でマテリアルを選択します。
ノードエディッタにgirl1_MBLab_anime_skinが表示されます。
表示されない場合はズーム等で調整してください。
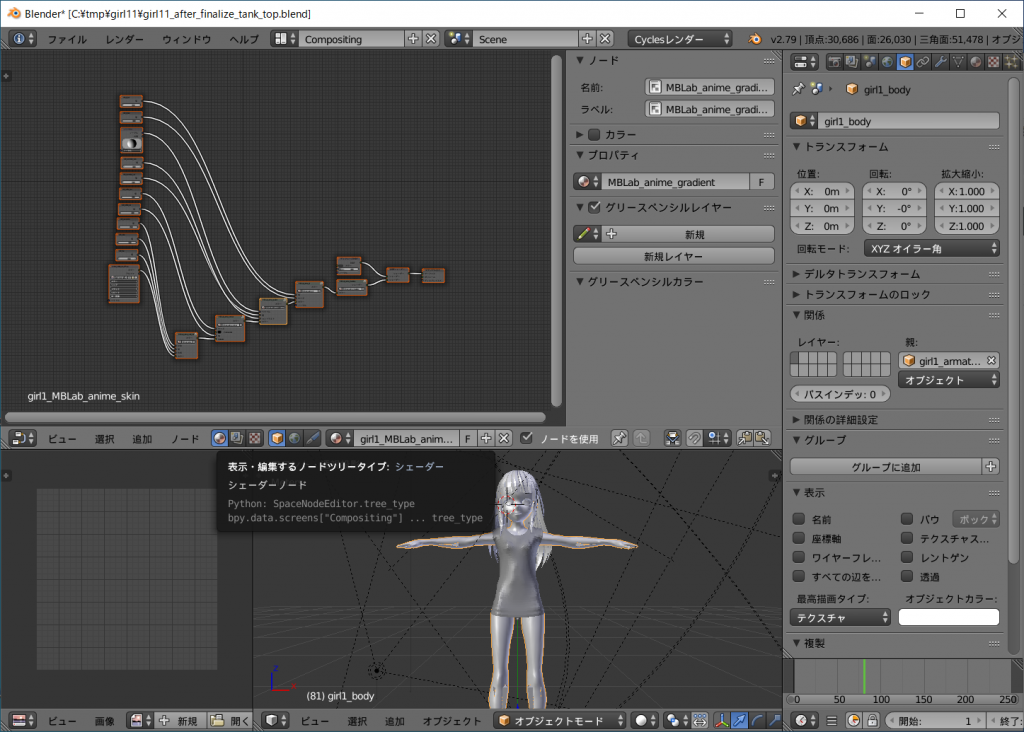
ノードエディッタウインドウの左上にマウスカーソルをあてて右ボタンを押したまま左下に動かすと矩形選択となりノード全てを選択することができます。
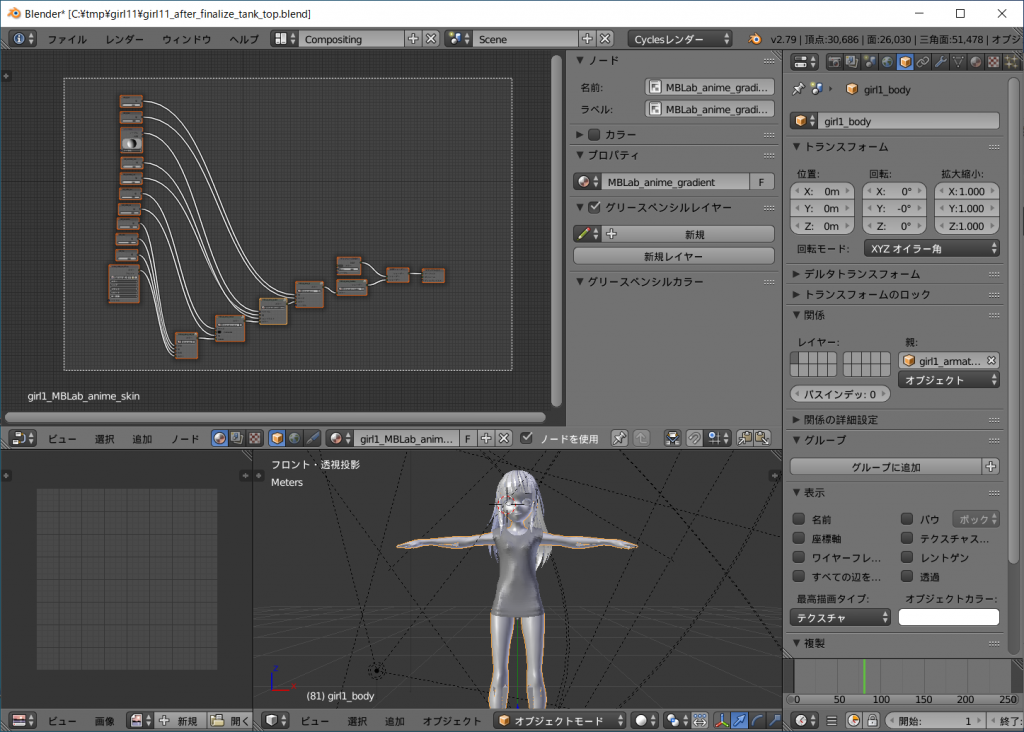
[ctrl]キーを押しながら[c]キーを押してコピーします。
次に3DビューエディッタウインドウTank_Top_Planeオブジェクトを右クリックして選択します。
ノードエディッタウインドウのマテリアルには何も設定されていない状態です。
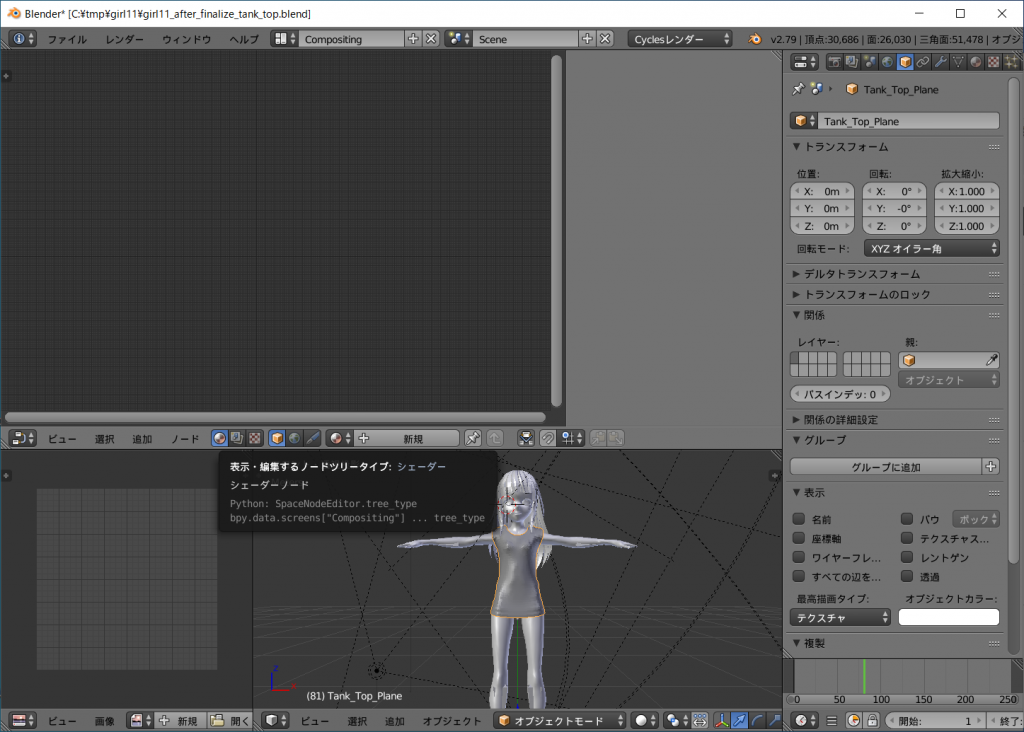
マテリアル選択の[新規]のボタンを左クリックすると新しいマテリアルが生成されます。
二つのノードが現れるのですが、これを[delete]キーで消します。
そしてノードエディッタウインドウにマウスカーソルを合わせて[ctrl]キーを押しながら[v]キーを押して、ノードをペーストします。
これで girl1_MBLab_anime_skinのノードがコピーされました。
ここで[Anime_mblab_skin_diffuse]を[RGB]に差し替えます。
ノードエディッタウインドウ上で[Anime_mblab_skin_diffuse] 付近をズームアップします。
[shift]キーを押しながら[a]キーを押すと[追加]メニューで出てくるので[入力] → [RGB]を辿り、選択します。
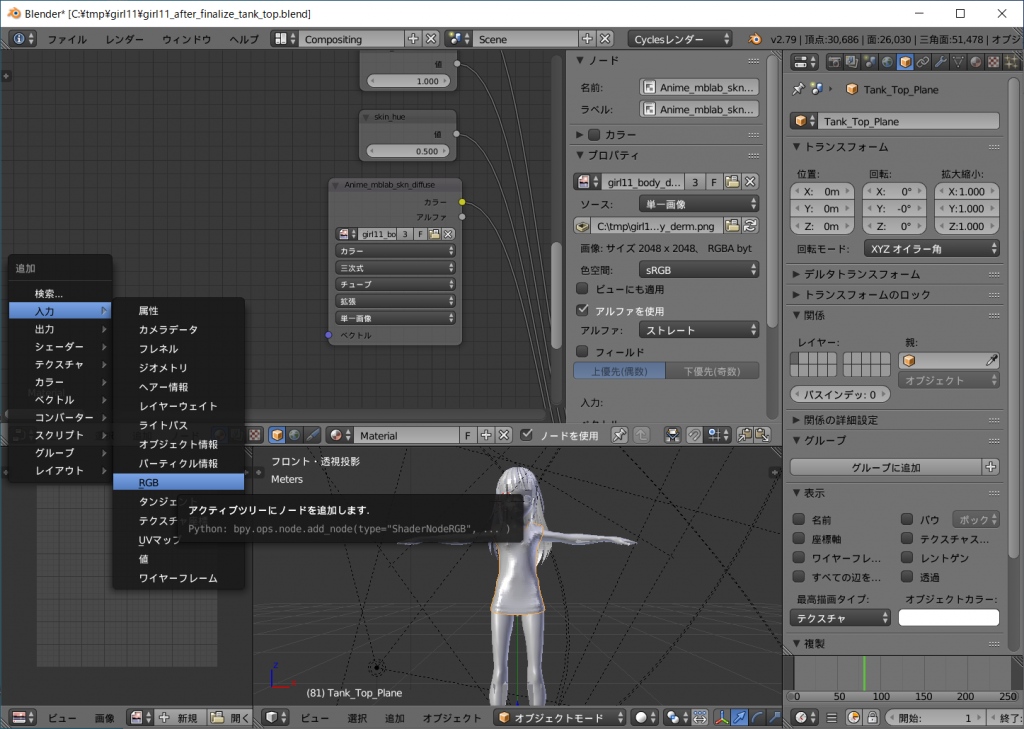
[RGB]ノードが現れるので出力[カラー]を繋ぎ変えます。
カラーサークルから適当な色を選択すると袖なしTシャツの色が自由に変えられます。
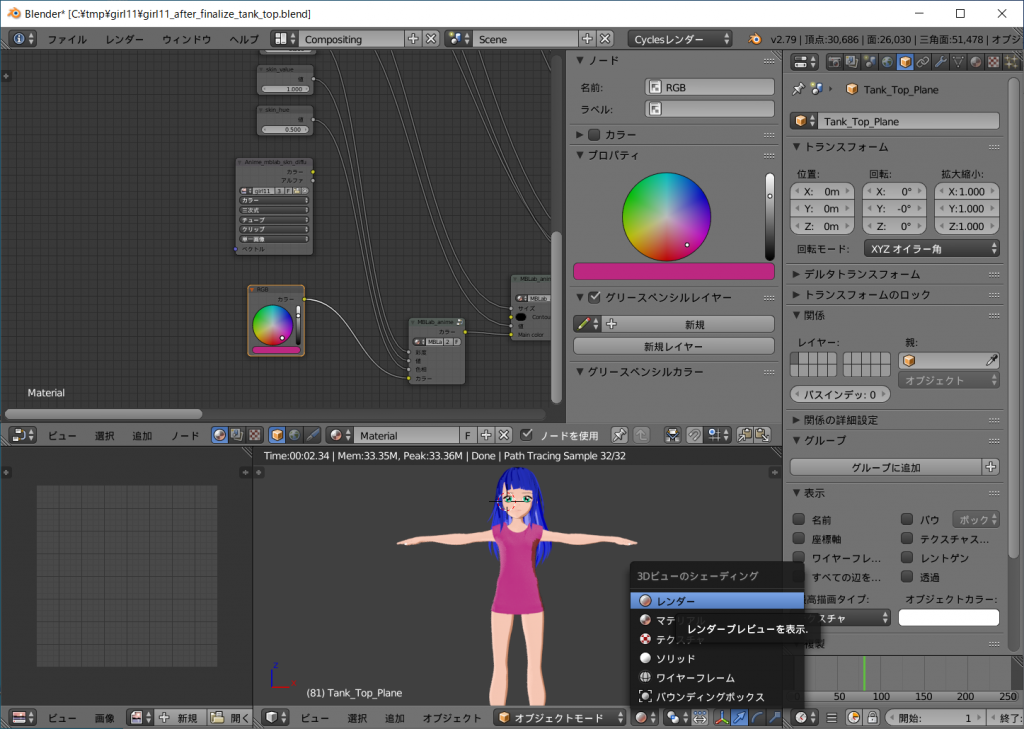
同様にオブジェクトウインドウでSendagaya_Shino_Hairオブジェクトを選択し、ノードエディットウインドウ上の[RGB]のカラーサークルを変えると、髪の色を任意に変えることができます。
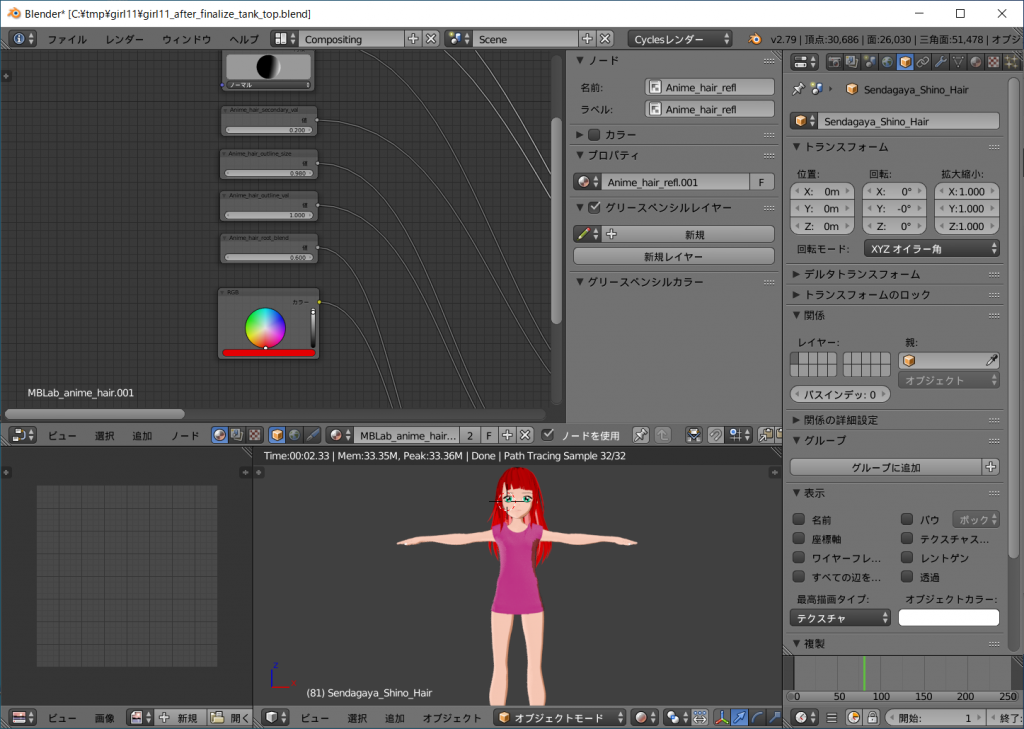
どうでしょうか?
メチャクチャ簡単だと思いませんか?
ここまで3D的な編集は殆どやっていません。
Blender、MB-Lab、VRoidStudioといった優れたソフトウェアを組み合わせることにより比較的自由に3Dキャラクターを生成できてしまいました。
これは凄いことなのです。

MB-LABの人体メッシュは秀逸です。
こんなにもクオリティの高いメッシュを使えるとは感謝しかありません。
VRoidStudioの髪型編集・作成機能を加えると強力この上ないソリューションとなります。
説明していませんが、設定されているマテリアルも良く考えられた応用の効くものです。
興味がおありでしたらノード構成を覗いて見られることをお勧めします。
今回はこれで終わりです。
絵は完成していませんが、時間があれば[その4]を書きたいと思います。