今回は完全に自分用のメモです。
Twitterを見ていて、Blenderのシェーダーノードでお絵かきしている方がいらっしゃったので追実験。
Blender 2.79bしか使えないのでノードは自作です。
なお、twの元ネタは以下であるようです。
楽しい!Unityシェーダー お絵描き入門!
Blenderで平面ポリゴンを追加して、その平面にシェーダーノードで図形を描写します。
凄く面白いアイデアであると思います。
構造は意外と簡単です。
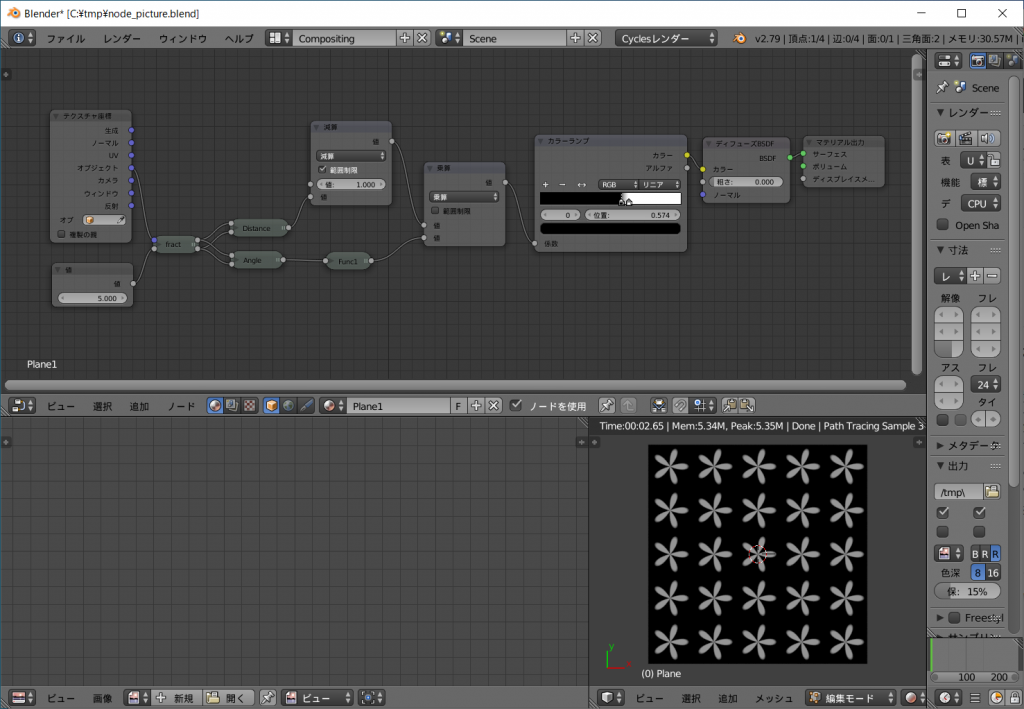
オブジェクトのテクスチャ画像からx,y各座標を取り出し、中央からの距離と角度を分離します。
そして距離と角度を入力パラメータとする関数を作成し て濃度グラフを作成します。
濃度にカラーランプノード等で閾値の範囲を決め、シェーダーで描写します。
等高線を取り出すノリですね。
fract, distance, angleの三つの ノードグループを作っています。
取り出すベクトルがレングス1.0に正規化されている前提としています。
fractは入力をオブジェクトのテクスチャ座標ベクトルとします。
各xyが周期1、レンジ-1.0~1.0の信号であると仮定し、任意倍数に逓倍し、新しいxy座標を個別に出力します。
出力の範囲は-1.0~1.0の実数です。
\(Fract(x,a) = mod(x+1.0 , \frac{2}{a})・\frac{a}{2} – 0.5\\
Fract(y,a) = mod(y+1.0 , \frac{2}{a})・ \frac{a}{2} – 0.5\)
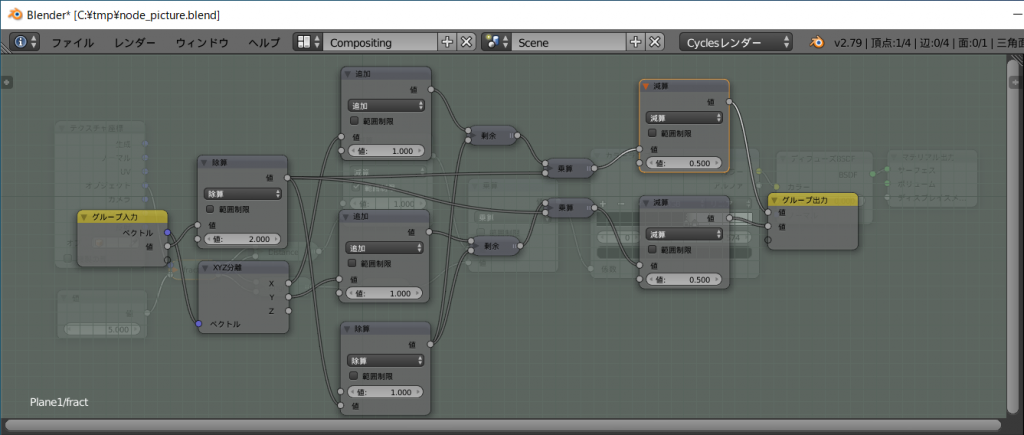
distanceは各xy座標を値として受け取り、原点からの距離を求めます。
出力の範囲は0.0~ \(\sqrt{2}\) の実数です
\(Distance(x,y)=\sqrt{x^2+y^2}\)
グループノードと出力をそのまま画像出力した例を以下に示します。
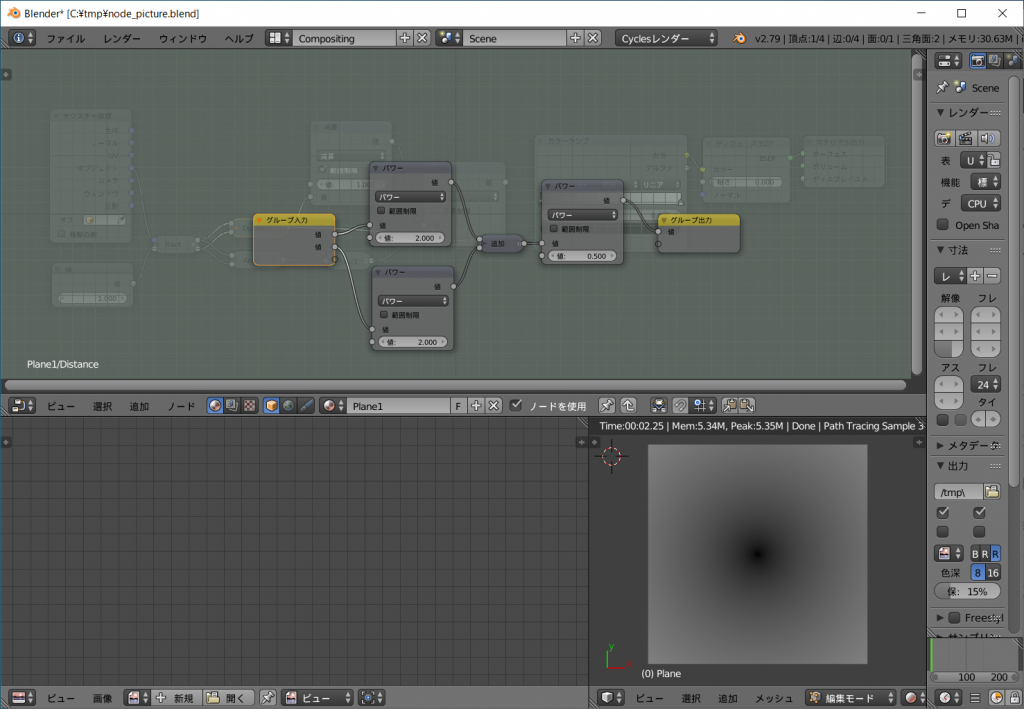
原点がゼロで値がゼロ、離れるに従い線形に値が増加してゆきます。
同じ距離であれば同じ値になります。
色表現的な意味では四隅は飽和していることに注意が必要です。
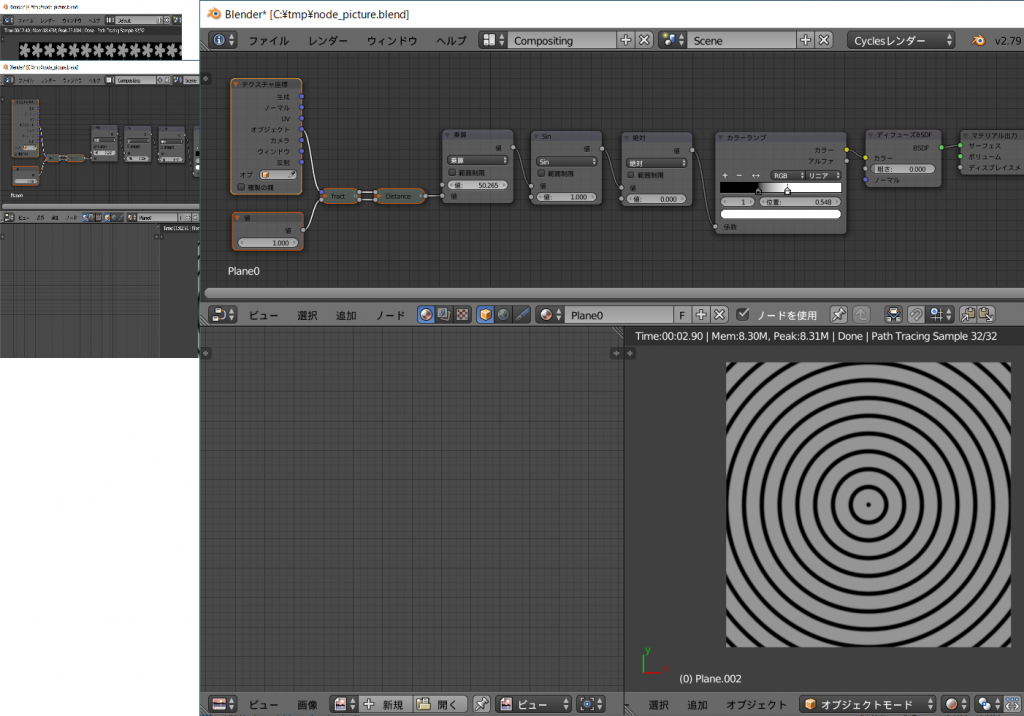
distanceを用いれば数式により同心円系の図形が描けます。
\(Func(s) = abs(sin(16πs))\)
angleは 各xy座標を値として受け取り、 原点との角度を計算します。
出力の範囲は \( 0.0~2π \)です。
\(Angle(x,y)=\\
cos^{-1}(\frac{x}{\sqrt{x^2+y^2} }) (if y ≧ 0)\\
Angle(x,y)=\\
cos^{-1}(\frac{-x}{\sqrt{x^2+y^2} })+π (if y < 0)\)
グループノードと出力を \( 2π \)で除して画像出力した例を以下に示します。
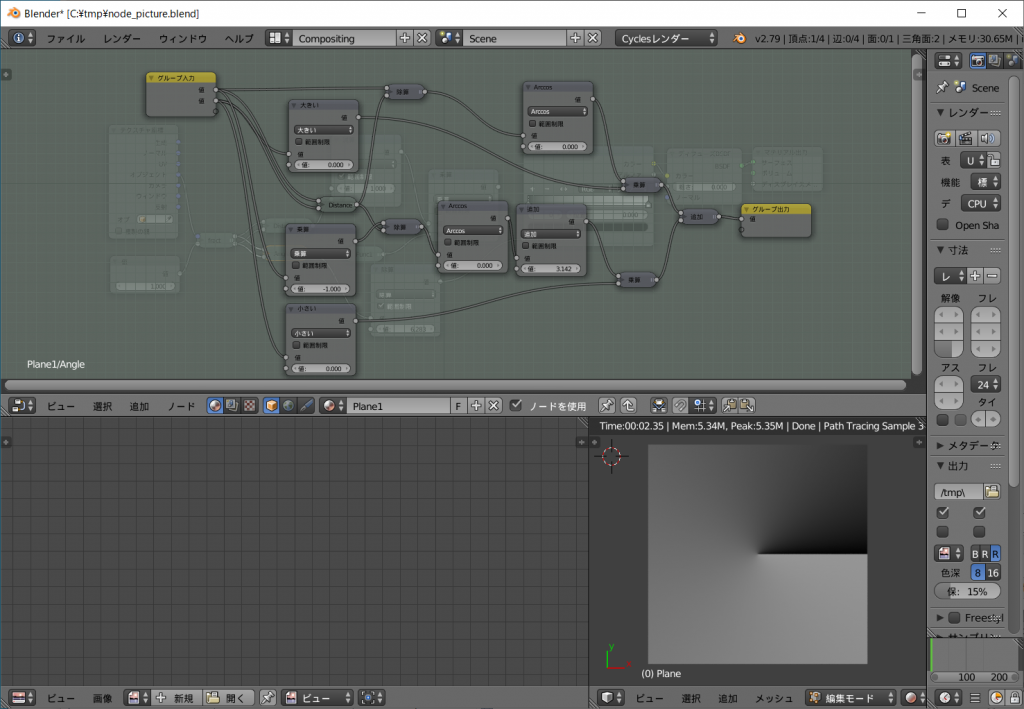
同じ角度であれば同じ値になり、反時計回りに値が増加してゆきます。
後はもう一つのノードグループfunc1に適当な関数を記述すれば良いわけです。
\(func1(s)=abs(cos(2.5s))\)
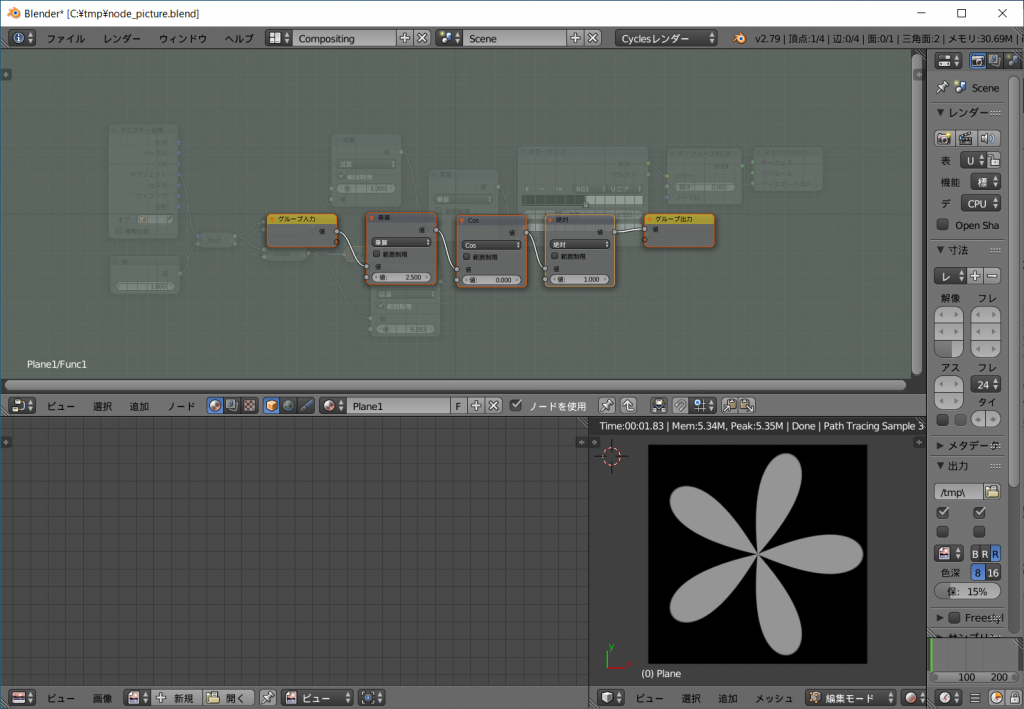
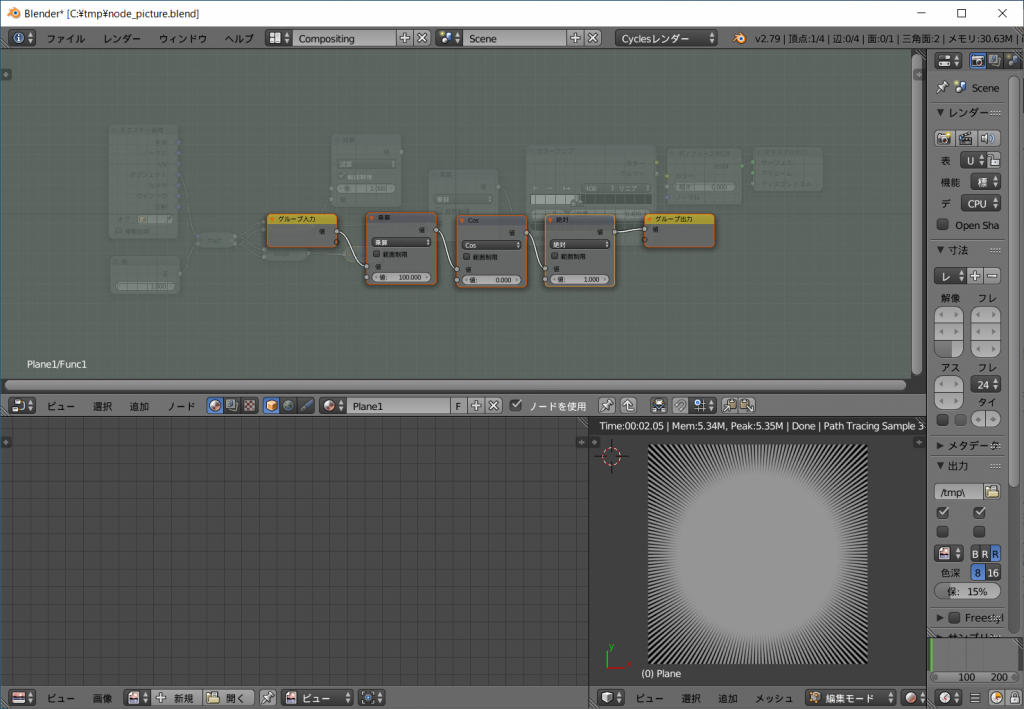
関数を設定してカラーランプノードを弄れば、抜きの入った集中線も実現できます。
\(func1(s)=abs(cos(100s))\)
桜の花びら。
\(Func2(s) = min(\\
abs(cos(2.5x))+0.4 ,\\
abs(sin(2.5x))+1.1)・0.240\)
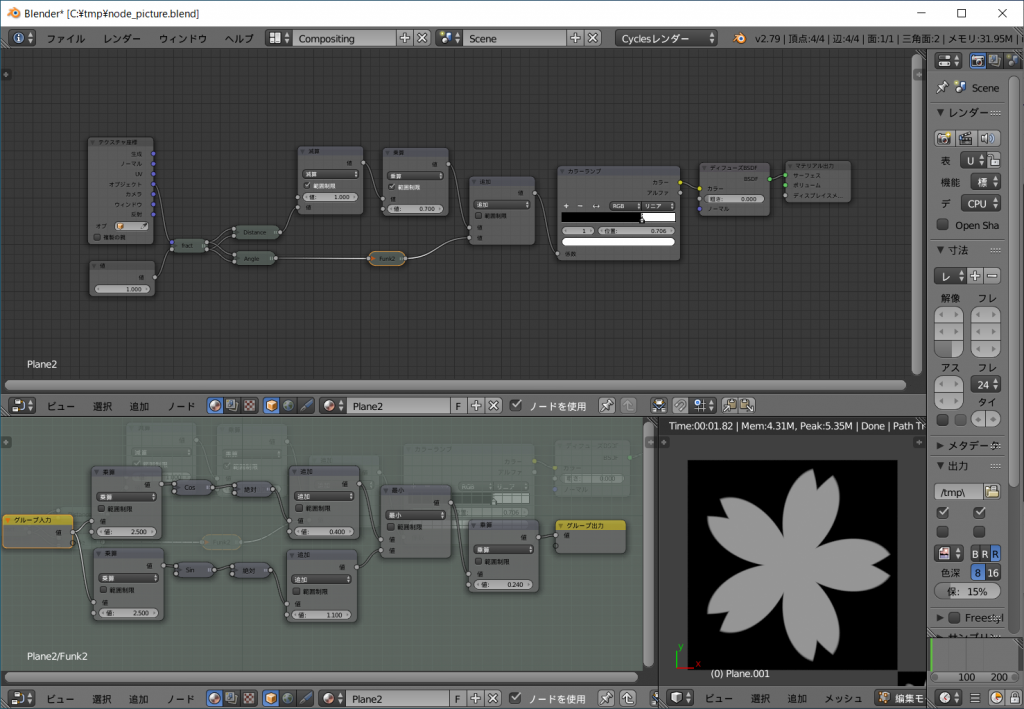
この作例ではDistance系とAngle系は乗算ではなく加算しています。
fractノードの入力を変えることにより任意の縮小繰り返しができます。
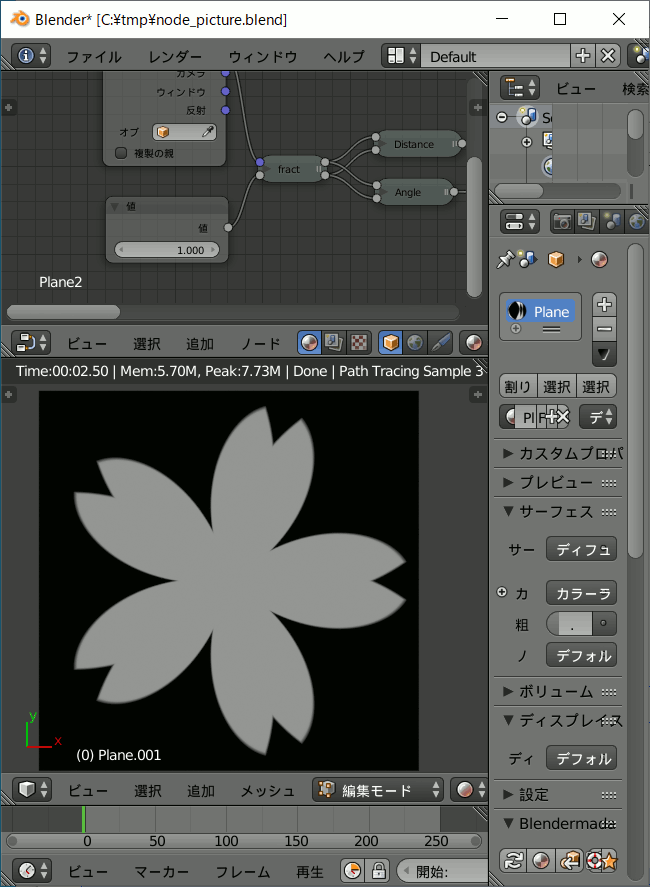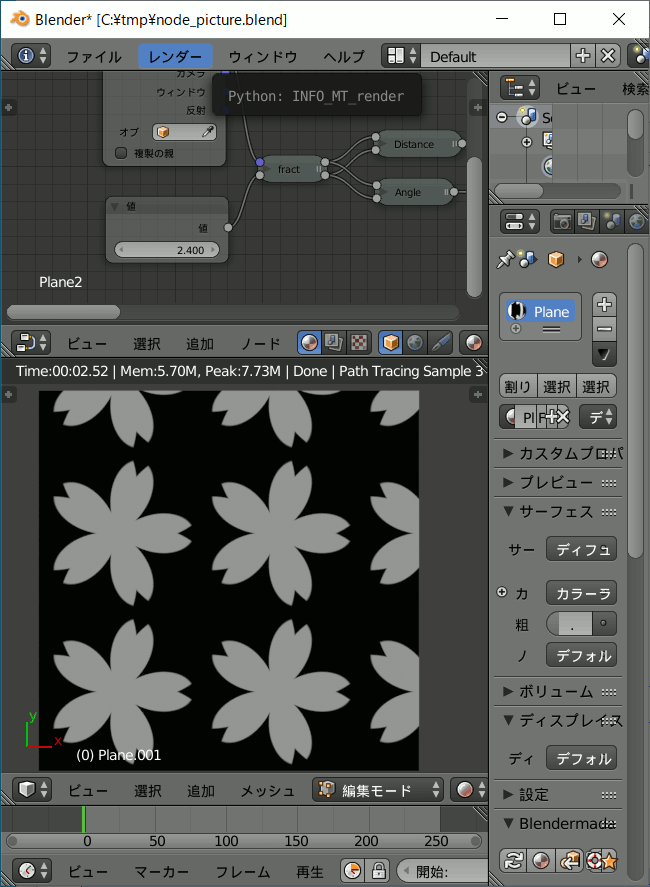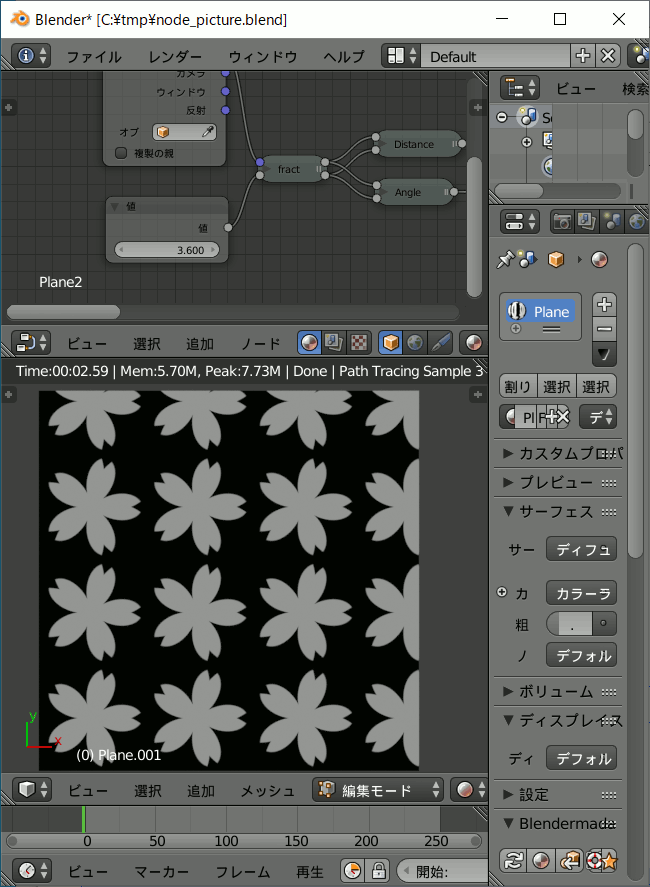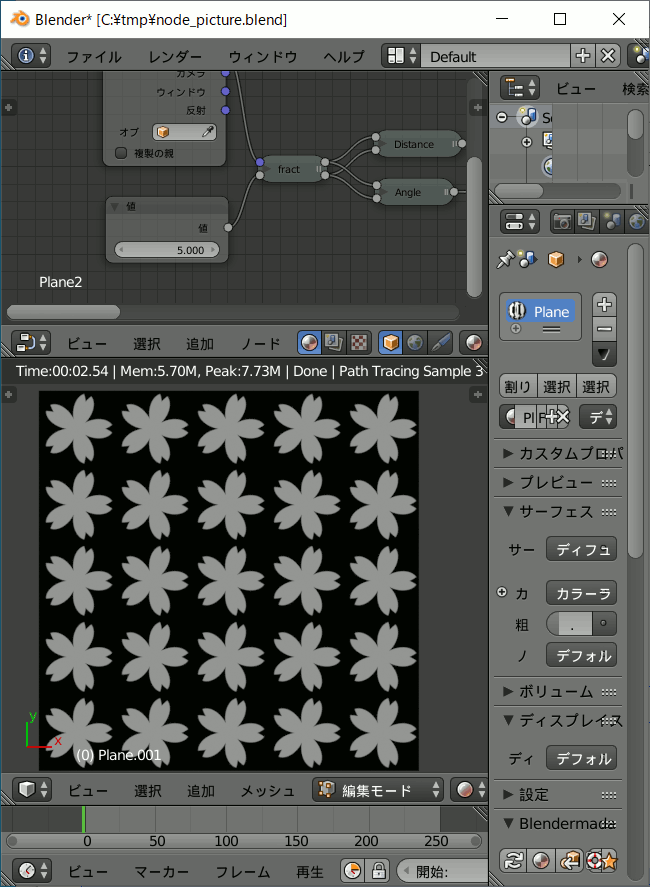
数式により任意の図形を作成し、それを繰り返しパターンにできるのです。
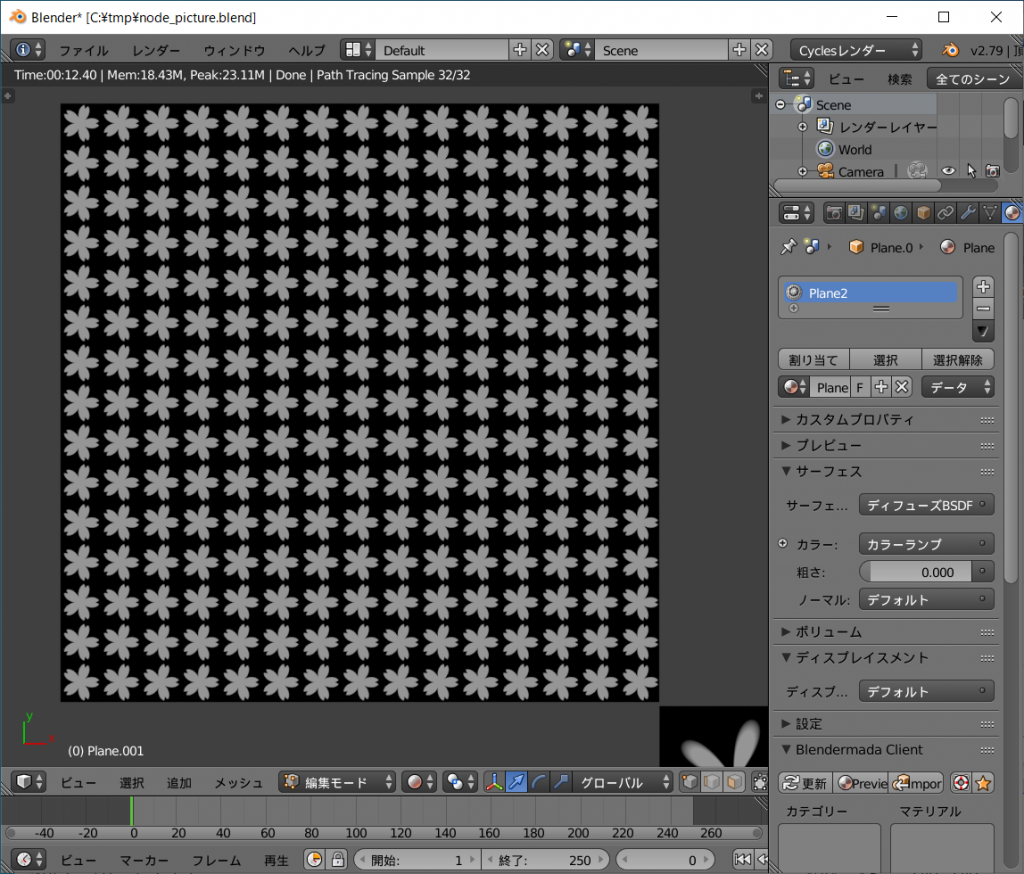
シェーダーノードはプログラム環境として機能し、様々な図形を描画できるところがとても興味深いです。
参考までにblenderファイルを置いておきます。
shader_node_sample.blend

